520+ câu hỏi trắc nghiệm Vật lí đại cương kèm đáp án và lời giải minh họa - Đề 5
49 câu hỏi 60 phút
Hai quả cầu kim loại tích điện trái dấu, treo trên hai sợi chỉ mảnh. Cho chúng chạm nhau rồi lại tách ra xa nhau thì hai quả cầu sẽ:
hút nhau, vì chúng tích điện trái dấu
đẩy nhau, vì chúng tích điện cùng dấu
không tương tác với nhau, vì chúng trung hòa về điện
Hoặc đẩy nhau, hoặc không tương tác với nhau nữa
Ban đầu, hai quả cầu tích điện trái dấu. Khi chúng chạm nhau, điện tích sẽ trung hòa một phần hoặc hoàn toàn, tùy thuộc vào điện dung của mỗi quả cầu. Sau khi tách ra, nếu điện tích vẫn còn (dù ít), chúng sẽ tích điện cùng dấu (dấu của quả cầu ban đầu có điện tích lớn hơn) và đẩy nhau. Nếu điện tích trung hòa hoàn toàn, chúng sẽ không tương tác nữa. Vì vậy, đáp án đúng là "hoặc đẩy nhau, hoặc không tương tác với nhau nữa."
Danh sách câu hỏi:
Ban đầu, hai quả cầu tích điện trái dấu. Khi chúng chạm nhau, điện tích sẽ trung hòa một phần hoặc hoàn toàn, tùy thuộc vào điện dung của mỗi quả cầu. Sau khi tách ra, nếu điện tích vẫn còn (dù ít), chúng sẽ tích điện cùng dấu (dấu của quả cầu ban đầu có điện tích lớn hơn) và đẩy nhau. Nếu điện tích trung hòa hoàn toàn, chúng sẽ không tương tác nữa. Vì vậy, đáp án đúng là "hoặc đẩy nhau, hoặc không tương tác với nhau nữa."
Ban đầu, hai quả cầu hút nhau nên q1 và q2 trái dấu.
Lực hút ban đầu: F1 = k|q1q2|/r2 = k|2.10-6.(-4).10-6|/r2 = 16 N (1)
Khi cho hai quả cầu chạm nhau, điện tích của mỗi quả cầu sau khi chạm là: q = (q1 + q2)/2 = (2.10-6 - 4.10-6)/2 = -1.10-6 C
Sau khi đưa về vị trí cũ, hai quả cầu đẩy nhau với lực:
F2 = k|q2|/r2 = k|( -1.10-6)2|/r2 = k.10-12/r2 (2)
Lấy (2) chia (1) ta được: F2/F1 = (k.10-12/r2)/(8.k.10-12/r2) = 1/8
=> F2 = F1/8 = 16/8 = 2N.
Vậy, hai quả cầu đẩy nhau với một lực 2N.
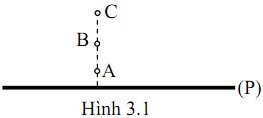
Xét vị trí của Q trên các đoạn:
- Nếu Q đặt trên đoạn x - q1: Lực do q1 tác dụng lên Q đẩy (vì cùng dấu), lực do q2 hút Q. Vì Q gần q1 hơn nên lực đẩy lớn hơn lực hút. Vậy lực tổng hợp tác dụng lên Q hướng về phía x (ra xa q1).
- Nếu Q đặt trên đoạn q1 - q2: Lực do q1 tác dụng lên Q đẩy, lực do q2 hút Q. Vậy lực tổng hợp tác dụng lên Q hướng về phía q2.
- Nếu Q đặt trên đoạn q2 - y: Lực do q1 tác dụng lên Q đẩy, lực do q2 hút Q. Vì Q gần q2 hơn nên lực hút lớn hơn lực đẩy. Vậy lực tổng hợp tác dụng lên Q hướng về phía q2 (ra xa q2).
Vậy cả a, b, c đều đúng trong một số trường hợp.
1. Điện trường do một vòng dây tích điện:
Xét một vòng dây tròn bán kính r, tích điện đều với điện tích Q. Điện trường tại một điểm M trên trục của vòng dây, cách tâm vòng dây một khoảng h, có độ lớn là:
\(E = \frac{kQh}{(r^2 + h^2)^{3/2}}\) với k là hằng số Coulomb.
2. Điện trường do vành khăn tích điện:
Vành khăn có thể coi là hợp của vô số vòng dây đồng tâm. Để tính điện trường do vành khăn gây ra, ta xét một vòng dây nhỏ bán kính \(r\) và độ dày \(dr\). Diện tích của vòng dây nhỏ này là \(dA = 2\pi r dr\). Mật độ điện tích mặt của vành khăn là \(\sigma = \frac{Q}{\pi (b^2 - a^2)}\), trong đó \(a\) và \(b\) là bán kính trong và bán kính ngoài của vành khăn.
Điện tích của vòng dây nhỏ là \(dQ = \sigma dA = \frac{Q}{\pi (b^2 - a^2)} 2\pi r dr = \frac{2Q}{b^2 - a^2} r dr\)
Điện trường do vòng dây nhỏ này gây ra tại điểm M là:
\(dE = \frac{k dQ h}{(r^2 + h^2)^{3/2}} = \frac{k h}{(r^2 + h^2)^{3/2}} \frac{2Q}{b^2 - a^2} r dr = \frac{2kQh}{b^2 - a^2} \frac{r dr}{(r^2 + h^2)^{3/2}}\
3. Tích phân để tìm điện trường tổng:
Để tìm điện trường tổng, ta tích phân \(dE\) từ \(a\) đến \(b\):
\(E = \int_{a}^{b} dE = \int_{a}^{b} \frac{2kQh}{b^2 - a^2} \frac{r dr}{(r^2 + h^2)^{3/2}} = \frac{2kQh}{b^2 - a^2} \int_{a}^{b} \frac{r dr}{(r^2 + h^2)^{3/2}}\
Đặt \(u = r^2 + h^2\), suy ra \(du = 2r dr\), do đó \(r dr = \frac{1}{2} du\). Khi \(r = a\) thì \(u = a^2 + h^2\), và khi \(r = b\) thì \(u = b^2 + h^2\).
Vậy:
\(E = \frac{2kQh}{b^2 - a^2} \int_{a^2 + h^2}^{b^2 + h^2} \frac{1}{2} u^{-3/2} du = \frac{kQh}{b^2 - a^2} \int_{a^2 + h^2}^{b^2 + h^2} u^{-3/2} du = \frac{kQh}{b^2 - a^2} [-2u^{-1/2}]_{a^2 + h^2}^{b^2 + h^2}\
\(E = \frac{kQh}{b^2 - a^2} [-2(b^2 + h^2)^{-1/2} + 2(a^2 + h^2)^{-1/2}] = \frac{2kQh}{b^2 - a^2} (\frac{1}{\sqrt{a^2 + h^2}} - \frac{1}{\sqrt{b^2 + h^2}})\
Vậy, biểu thức cường độ điện trường là:
\(E = \frac{{2kQh}}{{({b^2} - {a^2})}}(\frac{1}{{\sqrt {{a^2} + {h^2}} }} - \frac{1}{{\sqrt {{b^2} + {h^2}} }})\)
Theo định lý Gauss, thông lượng điện trường qua một mặt kín bằng tổng đại số các điện tích bên trong mặt kín chia cho hằng số điện môi của môi trường. Trong trường hợp này, môi trường là không khí, ta có thể coi hằng số điện môi bằng 1.
Tổng điện tích bên trong mặt kín (S) là: Q = Q1 + Q2 = 8μC + (-5μC) = 3μC
Vậy thông lượng điện cảm qua mặt (S) là 3μC.
.jpg)
.jpg)
.jpg)
.jpg)