520+ câu hỏi trắc nghiệm Vật lí đại cương kèm đáp án và lời giải minh họa - Đề 11
26 câu hỏi 60 phút
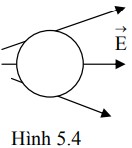
Một đĩa tròn bán kính R tích điện đều với mật độ điện tích mặt σ, đặt trong không khí. Phát biểu nào sau đây là SAI, khi nói về vectơ cường độ điện trường tại những điểm nằm trên trục, lân cận tâm O của đĩa?
Vuông góc với mặt phẳng của đĩa tròn
Hướng ra xa đĩa, nếu σ > 0
E = 0
Hướng lại gần đĩa, nếu σ < 0
* Phương: Vuông góc với mặt phẳng đĩa.
* Chiều: Hướng ra xa đĩa nếu điện tích dương (σ > 0), hướng lại gần đĩa nếu điện tích âm (σ < 0).
* Độ lớn: E ≠ 0 (trừ khi ở vô cùng).
Như vậy, phát biểu "E = 0" là sai.
Danh sách câu hỏi:
* Phương: Vuông góc với mặt phẳng đĩa.
* Chiều: Hướng ra xa đĩa nếu điện tích dương (σ > 0), hướng lại gần đĩa nếu điện tích âm (σ < 0).
* Độ lớn: E ≠ 0 (trừ khi ở vô cùng).
Như vậy, phát biểu "E = 0" là sai.
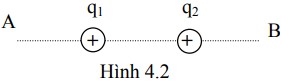
Phân tử lưỡng cực điện được tạo bởi hai điện tích trái dấu ±q đặt cách nhau một khoảng l. Vectơ mômen lưỡng cực điện ´p_e có:
- Phương: Trùng với đường thẳng nối hai điện tích.
- Chiều: Hướng từ điện tích âm sang điện tích dương.
- Độ lớn: p_e = q.l
Trong đó, q là độ lớn điện tích của mỗi ion, l là khoảng cách giữa chúng.
Vì mỗi ion có hoá trị 1, nên điện tích của mỗi ion bằng điện tích nguyên tố: q = 1,6.10^{-19} C.
Khoảng cách giữa hai ion là l = 10 nm = 10.10^{-9} m.
Vậy, độ lớn của mômen lưỡng cực điện là:
p_e = q.l = 1,6.10^{-19} C . 10.10^{-9} m = 1,6.10^{-27} Cm.
Và chiều của vectơ mômen điện là từ ion âm đến ion dương.
Câu hỏi này kiểm tra kiến thức về định nghĩa thông lượng điện trường qua một mặt bất kỳ. Thông lượng điện trường được tính bằng tích phân của tích vô hướng giữa vectơ cường độ điện trường \(\overrightarrow{E}\) và vectơ diện tích vi phân \(d\overrightarrow{S}\) trên toàn bộ bề mặt (S).
- Phương án 1: \({\Phi _E} = \int\limits_{(S)} {\overrightarrow E .d\,\overrightarrow S } \) Biểu thức này đúng vì nó thể hiện thông lượng điện trường là tích phân trên mặt (S) của tích vô hướng giữa cường độ điện trường và diện tích vi phân. Tuy nhiên, nó không nhấn mạnh rằng (S) là một mặt kín.
- Phương án 2: \({\Phi _E} = \oint\limits_{(S)} {\overrightarrow E .d\,\overrightarrow S } \) Biểu thức này đúng và đầy đủ hơn phương án 1. Kí hiệu \(\oint\) biểu thị tích phân trên một mặt kín (S), nhấn mạnh rằng thông lượng được tính qua một bề mặt kín.
- Phương án 3: \(d{\Phi _E} = \overrightarrow E .d\,\overrightarrow S \) Biểu thức này chỉ đúng cho thông lượng điện trường vi phân, tức là thông lượng qua một diện tích rất nhỏ dS. Nó không phải là biểu thức tính thông lượng điện trường tổng quát qua cả mặt (S).
- Phương án 4: \({\Phi _E} = \frac{1}{{\varepsilon {\varepsilon _0}}}\sum {{q_{i\,trong\,(S)}}} \) Biểu thức này thể hiện định lý Gauss, cho phép tính thông lượng điện trường qua một mặt kín (S) dựa vào tổng điện tích chứa bên trong mặt đó. Tuy nhiên, câu hỏi yêu cầu biểu thức *dùng để tính* thông lượng điện trường qua mặt (S) *bất kì*, nên định lý Gauss không phải là đáp án tổng quát nhất.
Phương án 2 chính xác nhất vì nó vừa là biểu thức tính thông lượng, vừa nhấn mạnh (S) là mặt kín, phù hợp với định nghĩa và ứng dụng thông thường của thông lượng điện trường.
Theo định luật Gauss cho điện trường, cảm ứng điện D tại một điểm gần mặt phẳng tích điện đều được tính bởi công thức:
D = σ / 2
trong đó σ là mật độ điện tích trên mặt phẳng.
Trong trường hợp này, σ = 2.10-8 C/m2.
Vậy, D = (2.10-8 C/m2) / 2 = 10-8 C/m2.
Vậy đáp án đúng là 10-8 C/m2 .
.jpg)
.jpg)
.jpg)