520+ câu hỏi trắc nghiệm Vật lí đại cương kèm đáp án và lời giải minh họa - Đề 7
48 câu hỏi 60 phút
Có 2 điện tích điểm q1, q2 bằng nhau nhưng trái dấu, đặt trên đường thẳng xy như hình 1.1. Đặt thêm điện tích điểm Q < 0 trên đường thẳng xy thì lực tác dụng lên Q có chiều:
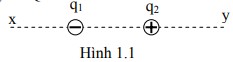
về phía x, nếu Q đặt trên đoạn x – q1
về phía y, nếu Q đặt trên đoạn q2 - y
về phiá q1, nếu Q đặt trên đoạn q1 – q2
a, b, c đều đúng
Phân tích lực tác dụng lên điện tích Q trong từng trường hợp:
- Nếu Q đặt trên đoạn x - q1: Lực hút của q1 lên Q sẽ lớn hơn lực đẩy của q2 lên Q (vì khoảng cách gần hơn). Do đó, lực tổng hợp sẽ hướng về phía q1, tức là về phía x.
- Nếu Q đặt trên đoạn q2 - y: Lực đẩy của q2 lên Q sẽ lớn hơn lực hút của q1 lên Q (vì khoảng cách gần hơn). Do đó, lực tổng hợp sẽ hướng ra xa q2, tức là về phía y.
- Nếu Q đặt trên đoạn q1 - q2: Lực hút của q1 lên Q hướng về phía q1, và lực đẩy của q2 lên Q cũng hướng về phía q1. Do đó, lực tổng hợp hướng về phía q1.
Vậy, cả a, b, c đều đúng.
Danh sách câu hỏi:
Phân tích lực tác dụng lên điện tích Q trong từng trường hợp:
- Nếu Q đặt trên đoạn x - q1: Lực hút của q1 lên Q sẽ lớn hơn lực đẩy của q2 lên Q (vì khoảng cách gần hơn). Do đó, lực tổng hợp sẽ hướng về phía q1, tức là về phía x.
- Nếu Q đặt trên đoạn q2 - y: Lực đẩy của q2 lên Q sẽ lớn hơn lực hút của q1 lên Q (vì khoảng cách gần hơn). Do đó, lực tổng hợp sẽ hướng ra xa q2, tức là về phía y.
- Nếu Q đặt trên đoạn q1 - q2: Lực hút của q1 lên Q hướng về phía q1, và lực đẩy của q2 lên Q cũng hướng về phía q1. Do đó, lực tổng hợp hướng về phía q1.
Vậy, cả a, b, c đều đúng.
Ban đầu, hai quả cầu đẩy nhau với lực F1 = k|q1q2|/r2. Vì q1 và q2 cùng dấu nên q1q2 > 0, do đó F1 = kq1q2/r2.
Sau khi cho hai quả cầu chạm nhau, điện tích của mỗi quả cầu là q = (q1 + q2)/2. Khi đưa chúng về vị trí cũ, chúng đẩy nhau với lực F2 = kq2/r2 = k(q1 + q2)2/(4r2).
Xét hiệu F2 - F1 = k/r2[(q1 + q2)2/4 - q1q2] = k/r2[q12 + 2q1q2 + q22 - 4q1q2]/4 = k/r2[q12 - 2q1q2 + q22]/4 = k(q1 - q2)2/(4r2).
Vì q1 ≠ q2 nên (q1 - q2)2 > 0, do đó F2 - F1 > 0, suy ra F2 > F1. Vậy chúng đẩy nhau với lực F2 > F1.
Để giải bài toán này, ta thực hiện các bước sau:
1. Tính cường độ điện trường do từng điện tích gây ra tại M:
- Cường độ điện trường do Q1 gây ra tại M: E1 = k|Q1|/r12, với r1 = MA = 0,1m
- Cường độ điện trường do Q2 gây ra tại M: E2 = k|Q2|/r22, với r2 = MB = 0,2m
2. Xác định phương và chiều của các vectơ cường độ điện trường:
- Vectơ E1 hướng ra xa Q1 (vì Q1 > 0)
- Vectơ E2 hướng về phía Q2 (vì Q2 < 0)
3. Tính góc giữa hai vectơ E1 và E2:
Vì MA = AB = 10cm, nên tam giác MAB là tam giác cân tại A. Do đó, góc \( \widehat{MAB} \)= 60o. Vì vectơ E1 hướng ra xa Q1 (A) và vectơ E2 hướng về phía Q2 (B), góc giữa hai vectơ này là 120o.
4. Tính cường độ điện trường tổng hợp tại M:
E = \( \sqrt{E_1^2 + E_2^2 + 2E_1E_2cos\alpha} \), với α là góc giữa E1 và E2.
Thay số:
- E1 = 9.109 * 8.10-6 / (0,1)2 = 7,2.106 V/m
- E2 = 9.109 * 6.10-6 / (0,2)2 = 1,35.106 V/m
- E = \( \sqrt{(7,2.10^6)^2 + (1,35.10^6)^2 + 2 * 7,2.10^6 * 1,35.10^6 * cos120^o} \) = 5,85.106 V/m
Điểm A(5, 0) cách gốc tọa độ O (nơi đặt điện tích -Q) một khoảng r_A = 5.
Điểm B(-2, -3) cách gốc tọa độ O một khoảng r_B = \sqrt{(-2)^2 + (-3)^2} = \sqrt{4 + 9} = \sqrt{13}.
Vì 5 = \sqrt{25} > \sqrt{13}, nên r_A > r_B. Do đó, E_A < E_B.

.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)