520+ câu hỏi trắc nghiệm Vật lí đại cương kèm đáp án và lời giải minh họa - Đề 8
50 câu hỏi 60 phút
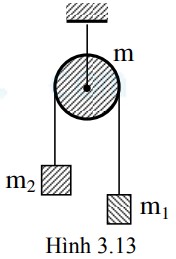
Hai quả cầu nhỏ giống hệt nhau, cùng khối lượng 0,1 g treo ở hai dây, mỗi dây dài 10 cm trong không khí, song song, hai quả cầu tiếp xúc nhau. Cho chúng tích điện q như nhau thì hai dây hợp với nhau góc 2α = 10014’. Lấy g = 10 m/s2 . Bán kính của chúng rất nhỏ so với chiều dài dây. Trị số q là:
1,8.10-9 C
3,6.10-9 C
1,8.10-8 C
0,9.10-9 C
Để giải bài toán này, ta cần phân tích lực tác dụng lên một trong hai quả cầu. Các lực tác dụng lên quả cầu bao gồm:
- Trọng lực P = mg, hướng xuống.
- Lực căng T của dây treo, hướng dọc theo dây.
- Lực đẩy tĩnh điện F giữa hai quả cầu, hướng ngang.
Vì hệ cân bằng, ta có:
tan(α) = F/P = F/(mg)
Với F = k*q2/r2, trong đó k = 9.109 Nm2/C2 là hằng số Coulomb, q là điện tích của mỗi quả cầu, và r là khoảng cách giữa hai quả cầu.
Từ hình vẽ, ta thấy r = 2l*sin(α), với l là chiều dài dây treo.
Vậy, tan(α) = (k*q2) / (mg*(2l*sin(α))2)
Suy ra, q2 = (mg * tan(α) * (2l*sin(α))2) / k
Cho α = 10°14’/2 = 5.07° ≈ 0.0884 rad (đổi sang radian để tính sin và tan)
sin(α) ≈ α = 0.0884
tan(α) ≈ α = 0.0884
m = 0.1 g = 0.1 * 10-3 kg
g = 10 m/s2
l = 10 cm = 0.1 m
Thay số vào, ta được:
q2 = (0.1*10-3 * 10 * 0.0884 * (2*0.1*0.0884)2) / (9*109)
q2 = (10-3 * 0.0884 * (0.01768)2) / (9*109)
q2 = (10-3 * 0.0884 * 0.0003125824) / (9*109)
q2 = (2.762 * 10-8) / (9*109) ≈ 3.069 * 10-18
q = √(3.069 * 10-18) ≈ 1.75 * 10-9 C
Giá trị này gần nhất với đáp án 1.8 * 10-9 C.
Danh sách câu hỏi:
Để giải bài toán này, ta cần phân tích lực tác dụng lên một trong hai quả cầu. Các lực tác dụng lên quả cầu bao gồm:
- Trọng lực P = mg, hướng xuống.
- Lực căng T của dây treo, hướng dọc theo dây.
- Lực đẩy tĩnh điện F giữa hai quả cầu, hướng ngang.
Vì hệ cân bằng, ta có:
tan(α) = F/P = F/(mg)
Với F = k*q2/r2, trong đó k = 9.109 Nm2/C2 là hằng số Coulomb, q là điện tích của mỗi quả cầu, và r là khoảng cách giữa hai quả cầu.
Từ hình vẽ, ta thấy r = 2l*sin(α), với l là chiều dài dây treo.
Vậy, tan(α) = (k*q2) / (mg*(2l*sin(α))2)
Suy ra, q2 = (mg * tan(α) * (2l*sin(α))2) / k
Cho α = 10°14’/2 = 5.07° ≈ 0.0884 rad (đổi sang radian để tính sin và tan)
sin(α) ≈ α = 0.0884
tan(α) ≈ α = 0.0884
m = 0.1 g = 0.1 * 10-3 kg
g = 10 m/s2
l = 10 cm = 0.1 m
Thay số vào, ta được:
q2 = (0.1*10-3 * 10 * 0.0884 * (2*0.1*0.0884)2) / (9*109)
q2 = (10-3 * 0.0884 * (0.01768)2) / (9*109)
q2 = (10-3 * 0.0884 * 0.0003125824) / (9*109)
q2 = (2.762 * 10-8) / (9*109) ≈ 3.069 * 10-18
q = √(3.069 * 10-18) ≈ 1.75 * 10-9 C
Giá trị này gần nhất với đáp án 1.8 * 10-9 C.
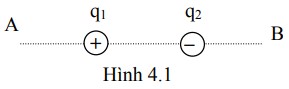
Để ba viên bi nhỏ tích điện nằm yên trên mặt bàn trơn nhẵn, tổng hợp lực tác dụng lên mỗi viên bi phải bằng 0. Điều này có nghĩa là các lực đẩy và hút giữa các viên bi phải cân bằng nhau.
* Trường hợp 1: Tích điện cùng dấu: Để các viên bi nằm yên, chúng phải nằm ở ba đỉnh của một tam giác đều. Khi đó, lực đẩy giữa các cặp viên bi sẽ có độ lớn bằng nhau và hướng ra ngoài, tạo thành một hệ lực cân bằng tại mỗi đỉnh.
* Trường hợp 2: Tích điện không cùng dấu: Để các viên bi nằm yên, chúng không thể nằm ở ba đỉnh của tam giác đều, vì khi đó lực hút giữa các cặp điện tích trái dấu sẽ hướng vào nhau, không tạo thành hệ lực cân bằng. Chúng phải nằm trên một đường thẳng, với một điện tích trái dấu nằm giữa hai điện tích cùng dấu. Lúc này, lực hút và lực đẩy có thể cân bằng nhau.
Vậy, đáp án đúng là "Tích điện không cùng dấu, nằm trên một đường thẳng."
- Độ lớn: E = k|Q|/r^2, tức là tỉ lệ nghịch với bình phương khoảng cách r từ Q đến M.
- Phương: trùng với đường thẳng nối Q và M.
- Chiều:
+ Hướng ra xa Q nếu Q > 0.
+ Hướng về phía Q nếu Q < 0.
Xét các phương án:
- Phương án 1: Sai vì cường độ điện trường tỉ lệ nghịch với bình phương khoảng cách.
- Phương án 2: Sai vì cường độ điện trường là đặc trưng riêng của điện trường tại điểm M, không phụ thuộc vào điện tích thử q đặt tại đó.
- Phương án 3: Đúng theo định nghĩa về chiều của cường độ điện trường.
- Phương án 4: Sai vì không phải tất cả các phương án a, b, c đều đúng.
Vậy, chỉ có phương án 3 đúng.
Ta có công thức tính cường độ điện trường tại tâm O do một dây cung tròn tích điện đều gây ra là:
\(E = \frac{{2k\lambda }}{R}\sin \frac{{\alpha _0}}{2}\)
Trong đó:
* k là hằng số Coulomb.
* λ là mật độ điện dài.
* R là bán kính vòng cung.
* α0 là nửa góc mở của vòng cung.
Vậy đáp án đúng là: \(E = \frac{{2k\lambda }}{{R}}\sin {\alpha _0}\)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)