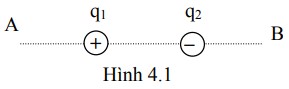
Hai quả cầu nhỏ giống hệt nhau, cùng khối lượng 0,1 g treo ở hai dây, mỗi dây dài 10 cm trong không khí, song song, hai quả cầu tiếp xúc nhau. Cho chúng tích điện q như nhau thì hai dây hợp với nhau góc 2α = 10⁰14’. Lấy g = 10 m/s² . Bán kính của chúng rất nhỏ so với chiều dài dây. Trị số q là:

1,8.10^-9 C

3,6.10^-9 C

1,8.10^-8 C

0,9.10^-9 C

Trả lời:

Đáp án đúng: A

520+ câu hỏi trắc nghiệm Vật lí đại cương kèm đáp án và lời giải minh họa - Phần 8

500+ câu hỏi ôn tập trắc nghiệm môn Vật lý đại cương sẽ là đề cương ôn thi hữu ích dành cho các bạn sinh viên Đại học - Cao đẳng ôn thi môn đại cương dễ dàng hơn. Mời các bạn cùng tham khảo!

50 câu hỏi 60 phút

Bắt đầu thi

Câu hỏi liên quan

Câu 2:

Đặt lên mặt bàn trơn nhẵn ba viên bi nhỏ tích điện, khối lượng không đáng kể thì chúng nằm yên. Ba viên bi đó phải có đặc điểm là:

Lời giải:

Đáp án đúng: D

Để ba viên bi nằm yên trên mặt bàn trơn nhẵn, tổng hợp lực tác dụng lên mỗi viên bi phải bằng 0. Điều này chỉ xảy ra khi các viên bi nằm ở vị trí cân bằng.

* Phương án 1: Nếu ba viên bi tích điện cùng dấu và ở ba đỉnh tam giác đều, chúng sẽ đẩy nhau. Tuy nhiên, do tính đối xứng của tam giác đều, lực đẩy tổng hợp lên mỗi viên bi sẽ hướng ra ngoài và khác 0, nên chúng không thể nằm yên. Do đó, phương án này sai.
* Phương án 2: Nếu ba viên bi tích điện cùng dấu và nằm trên một đường thẳng, hai viên bi ở hai đầu sẽ đẩy viên bi ở giữa. Viên bi ở giữa sẽ chịu lực đẩy tổng hợp khác 0 và không nằm yên. Do đó, phương án này sai.
* Phương án 3: Nếu ba viên bi tích điện không cùng dấu và nằm ở ba đỉnh tam giác đều, ta có thể chọn dấu của các viên bi sao cho lực tác dụng lên mỗi viên bi bằng 0. Ví dụ, nếu có hai viên bi tích điện dương và một viên bi tích điện âm, viên bi âm sẽ hút hai viên bi dương, và hai viên bi dương sẽ đẩy nhau. Với một điện tích phù hợp, hệ có thể cân bằng. Tuy nhiên, nếu 3 điện tích đều khác dấu thì không thể tạo thành tam giác đều cân bằng. Do đó, phương án này có thể đúng.
* Phương án 4: Nếu ba viên bi tích điện không cùng dấu và nằm trên một đường thẳng, điều kiện cân bằng có thể đạt được. Ví dụ, nếu hai viên bi ở hai đầu tích điện cùng dấu (ví dụ dương) và viên bi ở giữa tích điện trái dấu (ví dụ âm), lực hút của viên bi âm lên hai viên bi dương có thể cân bằng với lực đẩy giữa hai viên bi dương. Điều chỉnh khoảng cách và độ lớn điện tích có thể tạo ra trạng thái cân bằng. Vậy phương án này đúng.

Trong hai phương án 3 và 4, phương án 4 là phương án tổng quát hơn vì phương án 3 chỉ đúng khi có một điện tích trái dấu.

Vậy đáp án đúng là phương án 4.

Câu 3:

Phát biểu nào sau đây là đúng khi nói về cường độ điện trường tại điểm M, do điện tích điểm Q gây ra?

Lời giải:

Đáp án đúng: C

Cường độ điện trường tại một điểm M do điện tích điểm Q gây ra được định nghĩa là:

- Độ lớn: E = k|Q|/r^2, tức là tỉ lệ nghịch với bình phương khoảng cách r từ Q đến M.
- Phương: trùng với đường thẳng nối Q và M.
- Chiều:
+ Hướng ra xa Q nếu Q > 0.
+ Hướng về phía Q nếu Q < 0.

Xét các phương án:
- Phương án 1: Sai vì cường độ điện trường tỉ lệ nghịch với bình phương khoảng cách.
- Phương án 2: Sai vì cường độ điện trường là đặc trưng riêng của điện trường tại điểm M, không phụ thuộc vào điện tích thử q đặt tại đó.
- Phương án 3: Đúng theo định nghĩa về chiều của cường độ điện trường.
- Phương án 4: Sai vì không phải tất cả các phương án a, b, c đều đúng.

Vậy, chỉ có phương án 3 đúng.

Câu 4:

Dây mảnh hình vòng cung, bán kính R, góc mở 2α₀, tích điện đều, mật độ điện dài λ. Độ lớn cường độ điện trường E tại tâm O là:

Lời giải:

Đáp án đúng: D

Gọi dq là điện tích nhỏ trên vòng cung. Cường độ điện trường do dq gây ra tại tâm O là dE = k.dq/R^2. Vì vòng cung đối xứng qua trục Ox nên các thành phần dEy triệt tiêu lẫn nhau. Thành phần dEx = dE.sin(α) = k.dq.sin(α)/R^2. Ta có dq = λ.ds = λ.R.dα. Vậy Ex = ∫dEx = ∫(k.λ.sin(α).dα)/R (tích phân từ -α0 đến α0). Tính tích phân ta được Ex = (2kλsin(α0))/R. Vậy E = |Ex| = (2kλsin(α0))/R.

Câu 5:

Mặt phẳng (P) rộng vô hạn, tích điện đều với mật độ điện mặt σ. Cường độ điện trường do mặt phẳng này gây ra tại điểm M trong không khí, cách (P) một khoảng a được tính bởi biểu thức nào sau đây?

Lời giải:

Đáp án đúng: C

Điện trường do một mặt phẳng tích điện đều rộng vô hạn gây ra có độ lớn không đổi và được tính bằng công thức \(E = \frac{\sigma }{{{2\varepsilon _0}}}\), trong đó σ là mật độ điện mặt và ε₀ là hằng số điện môi. Do đó, đáp án đúng là phương án 3.

Câu 6:

Vectơ cảm ứng điện D ở bên ngoài không khí, gần mặt của tấm phẳng, khá rộng, bề dày d, tích điện đều với mật độ điện khối ρ có trị số là:

Lời giải:

Đáp án đúng: A

Áp dụng định lý Gauss cho một mặt Gauss hình trụ có một đáy nằm trong tấm phẳng và một đáy nằm ngoài không khí, gần mặt tấm phẳng. Điện tích chứa trong mặt Gauss là \(\rho Ad\), với A là diện tích đáy của hình trụ. Theo định lý Gauss, \(\oint {\overrightarrow D \cdot d\overrightarrow A } = Q\) . Vì điện trường chỉ tồn tại ở bên ngoài tấm phẳng và vuông góc với mặt phẳng, ta có \(DA = \rho Ad\) suy ra \(D = \rho d\).

Câu 7:

Điện tích Q = - 5μC đặt yên trong không khí. Điện tích q = +8μC di chuyển trên đường thẳng xuyên qua Q, từ M cách Q 40cm, ra xa Q thêm 20cm. Tính công của lực điện trường trong dịch chuyển đó.

Lời giải: