520+ câu hỏi trắc nghiệm Vật lí đại cương kèm đáp án và lời giải minh họa - Đề 2
50 câu hỏi 60 phút
Lực tương tác giữa 2 điện tích điểm sẽ thay đổi thế nào nếu ta cho độ lớn của mỗi điện tích điểm đó tăng gấp đôi, đồng thời khoảng cách gữa chúng cũng tăng gấp đôi?
Tăng gấp đôi
Giảm một nửa
Không đổi
Tăng gấp 4 lần
Lực tương tác giữa hai điện tích điểm được tính theo định luật Coulomb: F = k * |q1*q2| / r^2, trong đó k là hằng số Coulomb, q1 và q2 là độ lớn của hai điện tích, và r là khoảng cách giữa chúng.
Khi độ lớn của mỗi điện tích tăng gấp đôi (q1' = 2q1, q2' = 2q2) và khoảng cách giữa chúng cũng tăng gấp đôi (r' = 2r), lực tương tác mới F' sẽ là:
F' = k * |(2q1)*(2q2)| / (2r)^2 = k * |4*q1*q2| / (4*r^2) = k * |q1*q2| / r^2 = F
Vậy, lực tương tác không đổi.
Danh sách câu hỏi:
Lực tương tác giữa hai điện tích điểm được tính theo định luật Coulomb: F = k * |q1*q2| / r^2, trong đó k là hằng số Coulomb, q1 và q2 là độ lớn của hai điện tích, và r là khoảng cách giữa chúng.
Khi độ lớn của mỗi điện tích tăng gấp đôi (q1' = 2q1, q2' = 2q2) và khoảng cách giữa chúng cũng tăng gấp đôi (r' = 2r), lực tương tác mới F' sẽ là:
F' = k * |(2q1)*(2q2)| / (2r)^2 = k * |4*q1*q2| / (4*r^2) = k * |q1*q2| / r^2 = F
Vậy, lực tương tác không đổi.
Để tính lực tương tác giữa hai điện tích điểm, ta sử dụng định luật Coulomb:
\(F = k \frac{|q_1 q_2|}{r^2}\)
Trong đó:
- \(F\) là lực tương tác giữa hai điện tích (N)
- \(k\) là hằng số Coulomb, có giá trị \(k = 9 \times 10^9 N.m^2/C^2\)
- \(q_1\) và \(q_2\) là độ lớn của hai điện tích (C)
- \(r\) là khoảng cách giữa hai điện tích (m)
Đổi đơn vị:
- \(q_1 = 3 \mu C = 3 \times 10^{-6} C\)
- \(q_2 = 12 \mu C = 12 \times 10^{-6} C\)
- \(r = 30 cm = 0,3 m\)
Thay số vào công thức:
\(F = 9 \times 10^9 \frac{|3 \times 10^{-6} \times 12 \times 10^{-6}|}{0,3^2} = 9 \times 10^9 \frac{36 \times 10^{-12}}{0,09} = 9 \times 10^9 \times 400 \times 10^{-12} = 3600 \times 10^{-3} = 3,6 N\)
Vậy lực tương tác giữa hai điện tích là 3,6 N.
Lực tĩnh điện giữa hai hạt alpha là lực đẩy vì chúng cùng mang điện tích dương. Lực hấp dẫn giữa hai hạt alpha luôn là lực hút. Cả hai lực này đều là lực xuyên tâm và có độ lớn tỉ lệ nghịch với bình phương khoảng cách giữa hai hạt. Do đó, đáp án A sai. Lực hấp dẫn không phụ thuộc vào môi trường, trong khi lực tĩnh điện có phụ thuộc vào hằng số điện môi của môi trường. Do đó, đáp án B sai. Lực tĩnh điện giữa hai hạt alpha là lực đẩy, còn lực hấp dẫn là lực hút. Do đó, đáp án C sai.
Vậy, đáp án đúng là D: Cả 3 đáp án kia sai.
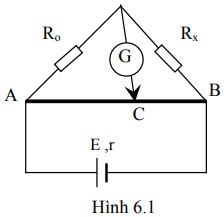
Để hệ ba điện tích nằm cân bằng, điện tích Q phải mang dấu dương (vì q1 và q2 đều âm) và nằm giữa q1 và q2. Gọi khoảng cách AC = x, CB = y.
Điện tích q1 cân bằng khi:
\(\dfrac{k|q_1Q|}{x^2} = \dfrac{k|q_1q_2|}{(x+y)^2} \Rightarrow \dfrac{|Q|}{x^2} = \dfrac{|q_2|}{(x+y)^2} \Rightarrow \dfrac{|Q|}{x^2} = \dfrac{|q|}{(x+y)^2}\) (1)
Điện tích q2 cân bằng khi:
\(\dfrac{k|q_2Q|}{y^2} = \dfrac{k|q_1q_2|}{(x+y)^2} \Rightarrow \dfrac{|Q|}{y^2} = \dfrac{|q_1|}{(x+y)^2} \Rightarrow \dfrac{|Q|}{y^2} = \dfrac{4|q|}{(x+y)^2}\) (2)
Từ (1) và (2) suy ra:
\(\dfrac{x^2}{y^2} = \dfrac{1}{4} \Rightarrow y = 2x\) hay CA = 2CB.
Vậy điểm C nằm trong đoạn thẳng AB và CA = 2CB.
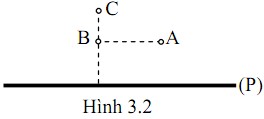
Lực do qB tác dụng lên qA là lực hút (do qA và qB trái dấu), có phương dọc theo AB, chiều từ A đến B. Độ lớn:
FB = k.|qA.qB| / AB² = 9.10^9 * |(-5.10^-8) * (16.10^-8)| / (0.08)² = 0,01125 N
Lực do qC tác dụng lên qA là lực hút (do qA và qC trái dấu), có phương dọc theo AC, chiều từ A đến C. Độ lớn:
FC = k.|qA.qC| / AC² = 9.10^9 * |(-5.10^-8) * (9.10^-8)| / (0.06)² = 0,01125 N
Vì tam giác ABC vuông tại A nên FAB và FAC vuông góc với nhau. Lực tổng hợp tác dụng lên qA là:
F = √(FB² + FC²) = √(0,01125² + 0,01125²) = 0,01125√2 N
Góc α hợp bởi F và AB được tính bằng:
tan(α) = FC / FB = 0,01125 / 0,01125 = 1
=> α = 45°
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)