200+ câu trắc nghiệm Lý thuyết điều khiển tự động có đáp án chi tiết

Câu 1:

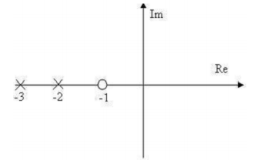
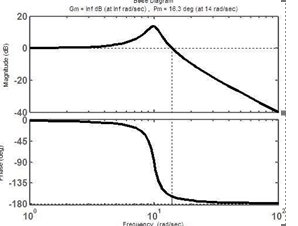
Hệ thống có các cực và zero như trên hình vẽ thì:

Lời giải:

Đáp án đúng: A

Hệ thống ổn định khi tất cả các cực (poles) của hàm truyền hệ thống nằm ở nửa mặt phẳng bên trái của mặt phẳng phức. Trong hình vẽ, ta thấy có một cực nằm ở phía bên phải mặt phẳng phức, do đó hệ thống không ổn định.

Câu 2:

Cho hàm truyền hãy lập phương trình trạng thái.\(G(s) = \frac{{20}}{{{s^2} + 2s + 8}}\)

Lời giải:

Đáp án đúng: C

Phương trình trạng thái có dạng:

\(\dot{x} = Ax + Bu\)
\(y = Cx + Du\)

Từ hàm truyền \(G(s) = \frac{20}{s^2 + 2s + 8}\), ta có phương trình vi phân:

\(Y(s)(s^2 + 2s + 8) = 20U(s)\)

\(\Rightarrow \ddot{y} + 2\dot{y} + 8y = 20u\)

Chọn trạng thái:

\(x_1 = y\)
\(x_2 = \dot{y}\)

Khi đó:

\(\dot{x_1} = \dot{y} = x_2\)

\(\dot{x_2} = \ddot{y} = -2\dot{y} - 8y + 20u = -2x_2 - 8x_1 + 20u\)

Phương trình trạng thái trở thành:

\(\begin{bmatrix} \dot{x_1} \\ \dot{x_2} \end{bmatrix} = \begin{bmatrix} 0 & 1 \\ -8 & -2 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} + \begin{bmatrix} 0 \\ 20 \end{bmatrix} u\)

\(y = \begin{bmatrix} 1 & 0 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix}\)

Vậy:

\(A = \begin{bmatrix} 0 & 1 \\ -8 & -2 \end{bmatrix}, B = \begin{bmatrix} 0 \\ 20 \end{bmatrix}, C = \begin{bmatrix} 1 & 0 \end{bmatrix}\)

Câu 3:

Khi thêm một cực có phần thực âm vào hàm truyền hệ hở thì:

Lời giải:

Đáp án đúng: C

Khi thêm một cực có phần thực âm vào hàm truyền hệ hở, quĩ đạo nghiệm số của hệ kín sẽ có xu hướng tiến về phía trục thực. Điều này làm tăng tính ổn định của hệ thống, vì các nghiệm của phương trình đặc tính (vị trí các cực của hệ kín) sẽ dịch chuyển về phía bên trái mặt phẳng phức, làm cho thời gian đáp ứng giảm và hệ thống ít dao động hơn. Do đó, độ dự trữ biên và độ dự trữ pha tăng lên, dẫn đến độ vọt lố giảm.

Câu 4:

ADC là:

Lời giải:

Đáp án đúng: C

ADC là viết tắt của Analog-to-Digital Converter, nghĩa là bộ chuyển đổi tín hiệu từ dạng tương tự sang dạng số. Thiết bị này thực hiện việc chuyển đổi một tín hiệu điện áp hoặc dòng điện liên tục (tương tự) thành một giá trị số rời rạc.

Câu 5:

Xét tính ổn định của hệ thống có phương trình đặc trưng: \({s^4} + 2{s^3} + 4{s^2} + 8s + 3 = 0\)

Lời giải:

Đáp án đúng: B

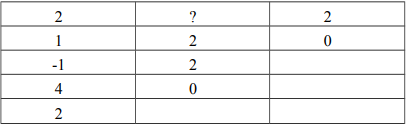
Để xét tính ổn định của hệ thống, ta sử dụng tiêu chuẩn Routh-Hurwitz. Ta lập bảng Routh như sau:

s^4 | 1 4 3
s^3 | 2 8 0
s^2 | (2*4 - 1*8)/2 = 0 (2*3 - 1*0)/2 = 3
s^1 | (0*8 - 2*3)/0 = -6/0 = ∞ (Do hàng s^2 có số 0 nên ta thay bằng ε và tiếp tục)
s^0 | 3

Hoặc ta có thể rút gọn hàng s^3 bằng cách chia cho 2 ta được:
s^4 | 1 4 3
s^3 | 1 4 0
s^2 | (1*4 - 1*4)/1 = 0 (1*3 - 1*0)/1 = 3
s^1 | (0*4 - 1*3)/0 = -3/0 = ∞ (Do hàng s^2 có số 0 nên ta thay bằng ε và tiếp tục)
s^0 | 3

Khi gặp số 0 ở cột đầu tiên, ta thay bằng ε, rồi tính tiếp các phần tử còn lại. Sau đó, ta xét dấu của cột đầu tiên khi ε -> 0. Trong trường hợp này, vì có sự đổi dấu ở cột đầu tiên (từ 0 sang một số âm khi ε tiến đến 0), hệ thống không ổn định.

Vậy, hệ thống không ổn định.