200+ câu trắc nghiệm Lý thuyết điều khiển tự động có đáp án - Đề 5
22 câu hỏi 60 phút
Nhấn để lật thẻ
1 / 22
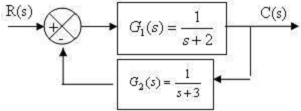
Hàm truyền đạt \(G(s) = \frac{{C(s)}}{{R(s)}}\) của hệ thống ở hình sau là:
A.
\(\frac{{{G_1}{G_2}{G_3}}}{{1 + {G_1}{G_2}{G_3}{G_4}}}\)
B.
\(\frac{{{G_1}{G_2}{G_3}}}{{1 - {G_1}{G_2}{G_3}{G_4}}}\)
C.
\(\frac{{{G_1}{G_2}}}{{1 + {G_1}{G_2}{G_3}{G_4}}}\)
D.
\(\frac{{{G_1}{G_2}{G_3}}}{{1 + {G_1}{G_2}{G_4}}}\)
Đáp án
Đáp án đúng: A
Để tìm hàm truyền đạt của hệ thống, ta áp dụng công thức cho hệ thống hồi tiếp âm. Hàm truyền đạt vòng kín của hệ thống hồi tiếp âm là:
\(G(s) = \frac{G_{forward}(s)}{1 + G_{forward}(s) * H(s)}\)
Trong đó:
- \(G_{forward}(s)\) là hàm truyền đạt của đường tiến (từ đầu vào R(s) đến đầu ra C(s)). Trong trường hợp này, \(G_{forward}(s) = G_1G_2G_3\).
- \(H(s)\) là hàm truyền đạt của đường hồi tiếp. Trong trường hợp này, \(H(s) = G_4\).
Vậy, hàm truyền đạt của hệ thống là:
\(G(s) = \frac{G_1G_2G_3}{1 + G_1G_2G_3G_4}\)
Vậy đáp án đúng là phương án 1.
\(G(s) = \frac{G_{forward}(s)}{1 + G_{forward}(s) * H(s)}\)
Trong đó:
- \(G_{forward}(s)\) là hàm truyền đạt của đường tiến (từ đầu vào R(s) đến đầu ra C(s)). Trong trường hợp này, \(G_{forward}(s) = G_1G_2G_3\).
- \(H(s)\) là hàm truyền đạt của đường hồi tiếp. Trong trường hợp này, \(H(s) = G_4\).
Vậy, hàm truyền đạt của hệ thống là:
\(G(s) = \frac{G_1G_2G_3}{1 + G_1G_2G_3G_4}\)
Vậy đáp án đúng là phương án 1.
Danh sách câu hỏi:
Lời giải:
Đáp án đúng: A
Để tìm hàm truyền đạt của hệ thống, ta áp dụng công thức cho hệ thống hồi tiếp âm. Hàm truyền đạt vòng kín của hệ thống hồi tiếp âm là:
\(G(s) = \frac{G_{forward}(s)}{1 + G_{forward}(s) * H(s)}\)
Trong đó:
- \(G_{forward}(s)\) là hàm truyền đạt của đường tiến (từ đầu vào R(s) đến đầu ra C(s)). Trong trường hợp này, \(G_{forward}(s) = G_1G_2G_3\).
- \(H(s)\) là hàm truyền đạt của đường hồi tiếp. Trong trường hợp này, \(H(s) = G_4\).
Vậy, hàm truyền đạt của hệ thống là:
\(G(s) = \frac{G_1G_2G_3}{1 + G_1G_2G_3G_4}\)
Vậy đáp án đúng là phương án 1.
\(G(s) = \frac{G_{forward}(s)}{1 + G_{forward}(s) * H(s)}\)
Trong đó:
- \(G_{forward}(s)\) là hàm truyền đạt của đường tiến (từ đầu vào R(s) đến đầu ra C(s)). Trong trường hợp này, \(G_{forward}(s) = G_1G_2G_3\).
- \(H(s)\) là hàm truyền đạt của đường hồi tiếp. Trong trường hợp này, \(H(s) = G_4\).
Vậy, hàm truyền đạt của hệ thống là:
\(G(s) = \frac{G_1G_2G_3}{1 + G_1G_2G_3G_4}\)
Vậy đáp án đúng là phương án 1.
Lời giải:
Đáp án đúng: D
Để hệ thống ổn định, ta sử dụng tiêu chuẩn Routh-Hurwitz. Lập bảng Routh:
s^4 | 1 1 K
s^3 | 12.5 5 0
s^2 | (12.5 - 5)/12.5=0.6 K 0
s^1 | (0.6*5 - 12.5*K)/0.6 0 0
s^0 | K 0 0
Để hệ thống ổn định, tất cả các phần tử ở cột đầu tiên của bảng Routh phải dương.
Điều kiện 1: 0.6 > 0 (luôn đúng)
Điều kiện 2: (3 - 12.5K)/0.6 > 0 => 3 - 12.5K > 0 => K < 3/12.5 = 0.24
Điều kiện 3: K > 0
Kết hợp các điều kiện, ta có 0 < K < 0.24
s^4 | 1 1 K
s^3 | 12.5 5 0
s^2 | (12.5 - 5)/12.5=0.6 K 0
s^1 | (0.6*5 - 12.5*K)/0.6 0 0
s^0 | K 0 0
Để hệ thống ổn định, tất cả các phần tử ở cột đầu tiên của bảng Routh phải dương.
Điều kiện 1: 0.6 > 0 (luôn đúng)
Điều kiện 2: (3 - 12.5K)/0.6 > 0 => 3 - 12.5K > 0 => K < 3/12.5 = 0.24
Điều kiện 3: K > 0
Kết hợp các điều kiện, ta có 0 < K < 0.24
Lời giải:
Đáp án đúng: B
Hàm truyền (Transfer Function) của một hệ thống là một khái niệm quan trọng trong lý thuyết điều khiển và kỹ thuật hệ thống. Nó được định nghĩa chính xác là tỉ số giữa biến đổi Laplace của tín hiệu ra và biến đổi Laplace của tín hiệu vào, với giả định điều kiện đầu bằng 0. Điều này có nghĩa là, nó mô tả mối quan hệ giữa tín hiệu đầu vào và đầu ra trong miền tần số (s-domain) khi hệ thống ở trạng thái nghỉ ban đầu.
* Phương án 1: "Là tỉ số giữa tín hiệu ra và tín hiệu vào" - Mặc dù có vẻ đúng, nhưng nó thiếu sự chính xác về mặt toán học. Hàm truyền được định nghĩa trong miền Laplace, không phải là tỉ số trực tiếp của tín hiệu trong miền thời gian.
* Phương án 2: "Là tỉ số giữa biến đổi Laplace của tín hiệu ra và biến đổi Laplace của tín hiệu vào khi điều kiện đầu bằng 0" - Đây là định nghĩa chính xác của hàm truyền.
* Phương án 3: "Phụ thuộc vào tín hiệu ra và tín hiệu vào" - Đúng là hàm truyền liên quan đến tín hiệu vào và ra, nhưng nó không chỉ đơn thuần là phụ thuộc mà là một mối quan hệ toán học cụ thể.
* Phương án 4: "Mô tả chức năng của các phần tử và sự tác động qua lại giữa chúng trong hệ" - Mô tả này thiên về mô hình hóa hệ thống hơn là định nghĩa hàm truyền.
Vậy, phương án đúng nhất là phương án 2.
* Phương án 1: "Là tỉ số giữa tín hiệu ra và tín hiệu vào" - Mặc dù có vẻ đúng, nhưng nó thiếu sự chính xác về mặt toán học. Hàm truyền được định nghĩa trong miền Laplace, không phải là tỉ số trực tiếp của tín hiệu trong miền thời gian.
* Phương án 2: "Là tỉ số giữa biến đổi Laplace của tín hiệu ra và biến đổi Laplace của tín hiệu vào khi điều kiện đầu bằng 0" - Đây là định nghĩa chính xác của hàm truyền.
* Phương án 3: "Phụ thuộc vào tín hiệu ra và tín hiệu vào" - Đúng là hàm truyền liên quan đến tín hiệu vào và ra, nhưng nó không chỉ đơn thuần là phụ thuộc mà là một mối quan hệ toán học cụ thể.
* Phương án 4: "Mô tả chức năng của các phần tử và sự tác động qua lại giữa chúng trong hệ" - Mô tả này thiên về mô hình hóa hệ thống hơn là định nghĩa hàm truyền.
Vậy, phương án đúng nhất là phương án 2.
Lời giải:
Đáp án đúng: C
Tiêu chuẩn IAE (Integral of the Absolute magnitude of the Error) là một tiêu chuẩn đánh giá chất lượng của hệ thống điều khiển dựa trên tích phân của trị tuyệt đối sai số theo thời gian. Công thức tổng quát của nó là tích phân từ 0 đến vô cùng của trị tuyệt đối của sai số e(t). Do đó, đáp án đúng là phương án 3.
Lời giải:
Đáp án đúng: A
Hàm truyền tương đương của hệ thống hồi tiếp âm đơn vị được tính theo công thức:
\(G_{td}(s) = \frac{G(s)}{1 + G(s)H(s)}\)
Trong đó, G(s) là hàm truyền của hệ thống hở và H(s) là hàm truyền của mạch hồi tiếp.
Trong trường hợp này, ta có G(s) = \(\frac{1}{s^2 + 5s + 4}\) và H(s) = s + 2.
Do đó,
\(G_{td}(s) = \frac{\frac{1}{s^2 + 5s + 4}}{1 + \frac{1}{s^2 + 5s + 4} * (s + 2)} = \frac{1}{s^2 + 5s + 4 + s + 2} = \frac{1}{s^2 + 6s + 6}\)
Tuy nhiên, không có đáp án nào trùng khớp với kết quả này. Có vẻ như đã có sai sót trong các phương án trả lời hoặc trong đề bài.
Nếu đề bài đúng, và ta có G(s) = 1/(s^2 + 5s + 4) và H(s) = s+2 thì kết quả đúng nhất phải là:
G_td(s) = G(s) / (1 + G(s)H(s)) = (1/(s^2 + 5s + 4)) / (1 + (1/(s^2+5s+4))*(s+2)) = 1 / (s^2 + 5s + 4 + s + 2) = 1 / (s^2 + 6s + 6)
Vì không có đáp án nào khớp, ta cần xem xét lại đề bài hoặc các phương án. Giả sử, nếu G(s) = 1/(s^2 + 5s + 4), để có một trong các đáp án, có lẽ cấu trúc hồi tiếp khác với hồi tiếp đơn vị âm thông thường.
Nếu đề bài cho G(s)H(s) và yêu cầu tính G_td(s) = G(s)/(1+G(s)H(s)) thì ta không đủ thông tin để giải. Trong trường hợp này, ta giả sử đề bài đúng như hình, và các đáp án có sai sót.
Tuy nhiên để chọn một đáp án "gần đúng nhất" thì ta thấy đáp án 4 có mẫu số gần với kết quả tính toán (sai số ở hệ số của s).
Như vậy, do có sự sai lệch trong đề bài hoặc các đáp án, không thể xác định đáp án chính xác theo lý thuyết.
\(G_{td}(s) = \frac{G(s)}{1 + G(s)H(s)}\)
Trong đó, G(s) là hàm truyền của hệ thống hở và H(s) là hàm truyền của mạch hồi tiếp.
Trong trường hợp này, ta có G(s) = \(\frac{1}{s^2 + 5s + 4}\) và H(s) = s + 2.
Do đó,
\(G_{td}(s) = \frac{\frac{1}{s^2 + 5s + 4}}{1 + \frac{1}{s^2 + 5s + 4} * (s + 2)} = \frac{1}{s^2 + 5s + 4 + s + 2} = \frac{1}{s^2 + 6s + 6}\)
Tuy nhiên, không có đáp án nào trùng khớp với kết quả này. Có vẻ như đã có sai sót trong các phương án trả lời hoặc trong đề bài.
Nếu đề bài đúng, và ta có G(s) = 1/(s^2 + 5s + 4) và H(s) = s+2 thì kết quả đúng nhất phải là:
G_td(s) = G(s) / (1 + G(s)H(s)) = (1/(s^2 + 5s + 4)) / (1 + (1/(s^2+5s+4))*(s+2)) = 1 / (s^2 + 5s + 4 + s + 2) = 1 / (s^2 + 6s + 6)
Vì không có đáp án nào khớp, ta cần xem xét lại đề bài hoặc các phương án. Giả sử, nếu G(s) = 1/(s^2 + 5s + 4), để có một trong các đáp án, có lẽ cấu trúc hồi tiếp khác với hồi tiếp đơn vị âm thông thường.
Nếu đề bài cho G(s)H(s) và yêu cầu tính G_td(s) = G(s)/(1+G(s)H(s)) thì ta không đủ thông tin để giải. Trong trường hợp này, ta giả sử đề bài đúng như hình, và các đáp án có sai sót.
Tuy nhiên để chọn một đáp án "gần đúng nhất" thì ta thấy đáp án 4 có mẫu số gần với kết quả tính toán (sai số ở hệ số của s).
Như vậy, do có sự sai lệch trong đề bài hoặc các đáp án, không thể xác định đáp án chính xác theo lý thuyết.
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Câu 9:
Phương trình vi phân biểu diễn khâu nguyên hàm với K là hệ số truyền của phần tử?
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP