200+ câu trắc nghiệm Lý thuyết điều khiển tự động có đáp án - Đề 2
50 câu hỏi 60 phút
Nhấn để lật thẻ
1 / 50
Hệ thống có hàm truyền: \(G(s) = \frac{{3(s + 4)}}{{{s^2} + 2s + 1}}\)
A.
z = -4 ; p1,2= -1
B.
z = 4; p1,2= 1
C.
z = 0 ; z = -4 ; p1,2= -1
D.
z = 4 ; p1,2= -1
Đáp án
Đáp án đúng: A
Danh sách câu hỏi:
Lời giải:
Đáp án đúng: A
Lời giải:
Đáp án đúng: C
Yêu cầu đầu tiên và quan trọng nhất đối với một hệ thống điều khiển tự động là tính ổn định. Hệ thống phải duy trì trạng thái ổn định, nghĩa là không dao động quá mức hoặc mất kiểm soát, khi chịu tác động của tín hiệu vào (tín hiệu điều khiển) và chịu ảnh hưởng của các nhiễu tác động lên hệ thống. Các yếu tố khác như tần số, tín hiệu ra không phải là yếu tố hàng đầu ảnh hưởng đến sự ổn định của hệ thống như nhiễu.
Lời giải:
Đáp án đúng: A
Phương trình đặc tính đã cho là một phương trình bậc hai: s² + 6s + 5 = 0. Ta có thể giải phương trình này bằng cách phân tích thành nhân tử hoặc sử dụng công thức nghiệm của phương trình bậc hai.
Phân tích thành nhân tử: s² + 6s + 5 = (s + 1)(s + 5) = 0.
Vậy, nghiệm của phương trình là s₁ = -1 và s₂ = -5.
Do đó, đáp án đúng là: s₁ = -1; s₂ = -5.
Phân tích thành nhân tử: s² + 6s + 5 = (s + 1)(s + 5) = 0.
Vậy, nghiệm của phương trình là s₁ = -1 và s₂ = -5.
Do đó, đáp án đúng là: s₁ = -1; s₂ = -5.
Lời giải:
Đáp án đúng: A
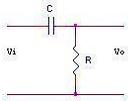
Để tìm hàm truyền đạt của mạch điện, ta cần xác định mối quan hệ giữa điện áp đầu ra Vo(s) và điện áp đầu vào Vi(s). Trong mạch này, điện trở R và tụ điện C tạo thành một mạch chia áp. Điện áp đầu ra Vo(s) chính là điện áp trên tụ điện.
Tổng trở của tụ điện là Zc = 1/(Cs).
Tổng trở của mạch là Z = R + 1/(Cs) = (RCs + 1)/(Cs).
Áp dụng công thức chia áp, ta có:
Vo(s) = Vi(s) * (Zc / Z) = Vi(s) * [1/(Cs)] / [(RCs + 1)/(Cs)] = Vi(s) * 1 / (RCs + 1).
Hàm truyền đạt G(s) = Vo(s) / Vi(s) = 1 / (RCs + 1).
Tuy nhiên, không có đáp án nào trùng khớp với kết quả này. Có lẽ có một lỗi trong đề bài hoặc các đáp án. Nếu mạch điện gồm một điện trở và tụ điện mắc nối tiếp, với điện áp ra lấy trên điện trở, thì hàm truyền đạt sẽ là: G(s) = R / (R + 1/(Cs)) = (RCs) / (RCs + 1).
Trong trường hợp này, đáp án A có vẻ là đáp án gần đúng nhất nếu điện áp ra được lấy trên điện trở. Vì vậy, ta chọn đáp án A với giả định rằng có một lỗi nhỏ trong sơ đồ hoặc cách lấy điện áp ra.
Tổng trở của tụ điện là Zc = 1/(Cs).
Tổng trở của mạch là Z = R + 1/(Cs) = (RCs + 1)/(Cs).
Áp dụng công thức chia áp, ta có:
Vo(s) = Vi(s) * (Zc / Z) = Vi(s) * [1/(Cs)] / [(RCs + 1)/(Cs)] = Vi(s) * 1 / (RCs + 1).
Hàm truyền đạt G(s) = Vo(s) / Vi(s) = 1 / (RCs + 1).
Tuy nhiên, không có đáp án nào trùng khớp với kết quả này. Có lẽ có một lỗi trong đề bài hoặc các đáp án. Nếu mạch điện gồm một điện trở và tụ điện mắc nối tiếp, với điện áp ra lấy trên điện trở, thì hàm truyền đạt sẽ là: G(s) = R / (R + 1/(Cs)) = (RCs) / (RCs + 1).
Trong trường hợp này, đáp án A có vẻ là đáp án gần đúng nhất nếu điện áp ra được lấy trên điện trở. Vì vậy, ta chọn đáp án A với giả định rằng có một lỗi nhỏ trong sơ đồ hoặc cách lấy điện áp ra.
Lời giải:
Đáp án đúng: C
Số nhánh của quỹ đạo nghiệm số bằng với bậc của đa thức mẫu số của hàm truyền hệ hở. Trong trường hợp này, mẫu số là (1 + 0.01s)^2, khi khai triển ra sẽ có bậc là 2. Vì vậy, số nhánh của quỹ đạo nghiệm số là 2.
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP