Trắc nghiệm Tích phân Toán Lớp 12

Câu 1:

Cho tích phân $I = \mathop \smallint \limits_2^3 \frac{{dx}}{{x\sqrt {{x^3} + 1} }}$. Xác định 3a+b biết $I = a\ln \left( {29 - 2\sqrt {27} } \right) + b\ln 3 + a\ln 2.$ $(a,b \in \mathbb{R})$

Câu 2:

Cho f(x) là hàm số chẵn và liên tục trên R thỏa mãn $\mathop \smallint \limits_{ - 1}^1 f\left( x \right)dx = 1$. Khi đó giá trị của tích phân $\mathop \smallint \limits_0^1 f\left( x \right)dx$ là:

Câu 3:

Cho f(x) liên tục trên [0;5] thỏa mãn $\mathop \smallint \limits_0^5 f\left( x \right)dx = 5,\mathop \smallint \limits_1^3 f\left( x \right)dx = 1$, khi đó giá trị của $P = \mathop \smallint \limits_0^1 f\left( x \right)dx + \mathop \smallint \limits_3^5 f\left( x \right)dx$ là:

Câu 4:

Số lượng một loại vi khuẩn gây bệnh có trong cơ thể của một người sau thời gian t (ngày) là f(t), trong đó $f'\left( t \right) = \frac{{10000}}{{3t + 1}}.$ Một người mắc bệnh do vi khuẩn gây ra. Khi đi khám lần thứ nhất, trong cơ thể của người này có 1000 con vi khuẩn nhưng lúc này cơ thể chưa phát bệnh. Biết rằng nếu trong cơ thể người đó có trên 12000 con vi khuẩn thì người này sẽ ở tình trạng nguy hiểm. Hỏi sau 10 ngày người đó đi khám lại thì trong cơ thể của họ có đang trong tình trạng nguy hiểm không, nếu có thì số lượng vi khuẩn vượt ngưỡng an toàn là bao nhiêu con?

Câu 5:

Tìm hệ số của số hạng chứa x⁹ trong khai triển nhị thức Newton $\left( {1 + 2x} \right){\left( {3 + x} \right)^{11}}.$

Câu 6:

Nếu $\text { Nếu } \int_{0}^{2}(2 x-3 f(x)) \mathrm{d} x=3 \text { thì } \int_{0}^{2} f(x) \mathrm{d} x$ bằng:

Câu 7:

Nếu $\int_{0}^{1}[3 f(x)+x] \mathrm{d} x=2 \text{ thì } \int_{0}^{1} f(x) \mathrm{d} x$ bằng:

Câu 8:

$\text { Nếu } \int_{0}^{2}(2 x-3 f(x)) \mathrm{d} x=3 \text { thì } \int_{0}^{2} f(x) \mathrm{d} x \text { bằng }$

Câu 9:

Biết $\int_{1}^{8} f(x) \mathrm{d} x=-2 ; \int_{1}^{4} f(x) \mathrm{d} x=3 ; \int_{1}^{4} g(x) \mathrm{d} x=7 .$. Mệnh đề nào sau đây sai?

Câu 10:

Biết rằng $\begin{equation} \int_{1}^{2} \frac{x^{3}-1}{x^{2}+x} \mathrm{~d} x=a+b \ln 3+c \ln 2 \text { với } a, b, c \text { là các số hữu tỉ. Tính } 2 a+3 b-4 c \text {. } \end{equation}$

Câu 11:

Giá trị của a để $\begin{equation} \int_{3}^{4} \frac{1}{(x-1)(x-2)} \mathrm{d} x=\ln a \end{equation}$ là:

Câu 12:

$\begin{equation} \text { Cho } \int_{-1}^{1}\left[5 f(x)+x^{2021}+x\right] \mathrm{d} x=20 \end{equation}$. $\begin{equation} \text { Tính } \int_{-1}^{1} f(x) \mathrm{d} x \text {. } \end{equation}$

Câu 13:

$\begin{equation} \text { Nếu } \int_{2}^{2021} f(x) d x=12 \text { và } \int_{2020}^{2021} f(x) d x=2 \end{equation}$ $\begin{equation} \text { thì } \int_{2}^{2020} f(x) d x \text { bằng } \end{equation}$

Câu 14:

Nếu $\begin{equation} \int_{-1}^{4}[5 f(x)-3] \mathrm{d} x=5 \text { thì } \int_{-1}^{4} f x \mathrm{~d} x \text { bằng } \end{equation}$

Câu 15:

$\begin{equation} \text { Biết } \int_{0}^{1} f(x) d x=\frac{1}{3} \text { và } \end{equation}$ $\begin{equation} \int_{0}^{1} g(x) d x=\frac{4}{3} . \text { Khi đó } \int_{0}^{1}(g(x)-f(x)) d x \text { bằng } \end{equation}$

Câu 16:

$\begin{equation} \text { Nếu } \int_{2}^{5} f(x) d x=10 \text { và } \end{equation}$$\begin{equation} \int_{2}^{9} f(x) d x=7 \text { thì } \int_{5}^{9} f(x) d x \text { bằng } \end{equation}$

Câu 17:

Cho hàm số $\begin{equation} f(x), g(x) \text { liên tục trên }[0 ; 1] \text { và } \int_{0}^{1} f(x) \mathrm{d} x=-1, \int_{0}^{1} g(x) \mathrm{d} x=2 \text {. Tính } \int_{0}^{1}[2 f(x)+3 g(x)] \mathrm{d} x \end{equation}$

Câu 18:

$\begin{equation} \text { Nếu } \int_{1}^{2} f(x) d x=3 \end{equation}$ $\begin{equation} \text { và } \int_{1}^{2} g(x) d x=-1 \text { thì } \int_{1}^{2}[2 f(x)+3 g(x)] d x \text { bằng } \end{equation}$

Câu 19:

Nếu $\int_{1}^{3}[f(x)-2 x] \mathrm{d} x=5 \text { thì } \int_{1}^{3} f(x) \mathrm{d} x \text { bằng }$

Câu 20:

$\text { Nếu } \int_{1}^{2} f(x) \mathrm{d} x=5$ $\text { và } \int_{1}^{2} g(x) \mathrm{d} x=9 \text { thì } \int_{1}^{2}[2 f(x)+g(x)] \mathrm{d} x \text { bằng }$

Câu 21:

Cho f(x);g(x) là các hàm số liên tục trên R thoả mãn $\int_{0}^{1} f(x) d x=3$, $\int_{0}^{2}[f(x)-3 g(x)] d x=4 \text { và } \int_{0}^{2}[2 f(x)+g(x)] d x=8$. $\text { Tính } \int_{1}^{2} f(x) d x$

Câu 22:

$\text { Nếu } \int_{0}^{1} f(x) \mathrm{d} x=3 \text { và } \int_{0}^{3} f(x) \mathrm{d} x=7$$\text { thì } \int_{1}^{3} f(x) \mathrm{d} x \text { bằng }$

Câu 23:

$\text { Tích phân } \int_{-1}^{1} x^{2020} d x \text { bằng }$

Câu 24:

Cho $\int_{0}^{1}[f(x)-2 g(x)] \mathrm{d} x=12 \text { và } \int_{0}^{1} g(x) \mathrm{d} x=5 \text {. Khi đó } \int_{0}^{1} f(x) \mathrm{d} x$ bằng:

Câu 25:

Cho hàm số f(x) thỏa mãn $\int_{0}^{1}(x+1) f^{\prime}(x) \mathrm{d} x=10 \text { và } 2 f(1)-f(0)=2 . \text { Tính } I=\int_{0}^{1} f(x) \mathrm{d} x .$
 

Câu 26:

Cho a là một số dương lớn hơn 1. Mệnh đề nào dưới đây sai?

Câu 27:

Cho tích phân $\mathop \smallint \limits_{\frac{\pi }{3}}^{\frac{\pi }{2}} \frac{{\sin x}}{{cosx + 2}}d{\rm{x}} = a\ln 5 + b\ln 2$ với a,b ∈Z.  Mệnh đề nào dưới đây đúng?

Câu 28:

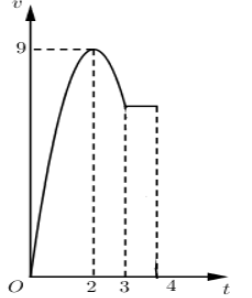
Một vật chuyển động trong 4 giờ với vân tốc v (km/h) phụ thuộc vào thời gian t (h) có đồ thị vận tốc như hình bên. Trong khoảng thời gian 3 giờ kể từ khi bắt đầu chuyển động, đồ thị đó là một phần của parabol có đỉnh I(2;9) với trục đối xứng song song với trục tung, khoảng thời gian còn lại đồ thị là một đoạn thẳng song song với trục hoành. Tính quãng đường s mà vật di chuyển được trong 4 giờ đó được :

Câu 29:

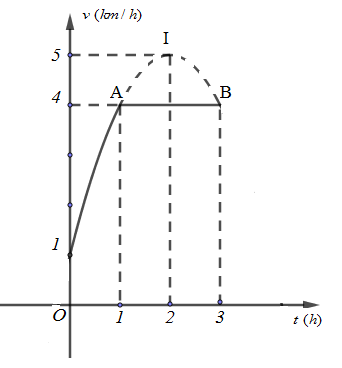
Một vật chuyển động trong 3 giờ với vận tốc v (km/h) phụ thuộc vào thời gian t (h) có đồ thị vận tốc như hình bên. Trong khoảng thời gian 1 giờ kể từ khi bắt đầu chuyển động, đồ thị đó là một phần của đường parabol có đỉnh I(2;5) và có trục đối xứng song song với trục tung, khoảng thời gian còn lại của đồ thị là một đoạn thẳng song song với trục hoành. Tính quãng đường mà vật di chuyển được trong 3 giờ đó

Câu 30:

Biết rằng $I = \mathop \smallint \limits_1^e \frac{{{{\ln }^2}x + \ln x}}{{{{\left( {\ln x + x + 1} \right)}^3}}}{\mkern 1mu} {\rm{d}}x = \frac{{a{e^2} + be - 12}}{{8{{(e + 2)}^2}}}$ với a, b là các số nguyên dương. Hiệu b - a bằng

Câu 31:

Cho hàm số $f(x) = \left\{ {\begin{array}{*{20}{l}} {{x^2} + x + 1}&{{\rm{ khi }}x \ge 0}\\ {2x - 3}&{{\rm{ khi }}x < 0} \end{array}} \right.$. Biết $I=\int\limits_{0}^{\frac{\pi }{2}}{f(2\sin x-1)\cos x~dx}+\int\limits_{e}^{{{e}^{2}}}{\frac{f\left( \ln x \right)}{x}dx}=\frac{a}{b}$ với $\frac{a}{b}$ là phân số tối giản. Giá trị của tích $a+b$ bằng

Câu 32:

Cho hàm số $f(x) = \left\{ {\begin{array}{*{20}{l}} {\frac{1}{2}x + 2}&{{\rm{ khi 0}} \le {\rm{x < 2}}}\\ { - x + 7}&{{\rm{ khi 2}} \le x < 5} \end{array}} \right.$. Biết $I=\int\limits_{1}^{{{e}^{2}}}{\frac{f\left( \ln x \right)}{x}}dx+\int\limits_{\sqrt{3}}^{2\sqrt{6}}{x.f\left( \sqrt{{{x}^{2}}+1} \right)}dx=\frac{a}{b}$ với $\frac{a}{b}$ là phân số tối giản. Giá trị của hiệu $a-b$ bằng

Câu 33:

Cho hàm số $f(x) = \left\{ {\begin{array}{*{20}{l}} {2{x^3} - x}&{{\rm{ khi }}x \ge 1}\\ { - 3x + 2}&{{\rm{ khi }}x < 1} \end{array}} \right.$. Biết $I=\int\limits_{\frac{\pi }{4}}^{\frac{\pi }{3}}{\frac{f\left( \tan x \right)}{{{\cos }^{2}}x}}dx+\int\limits_{0}^{\sqrt{\sqrt{e}-1}}{\frac{x.f\left( \ln \left( {{x}^{2}}+1 \right) \right)}{{{x}^{2}}+1}}dx=\frac{a}{b}$với $\frac{a}{b}$ là phân số tối giản. Giá trị của tổng $a+b$ bằng

Câu 34:

Cho hàm số $f(x) = \left\{ {\begin{array}{*{20}{l}} {4x}&{{\rm{ khi }}x > 2}\\ { - 2x + 12}&{{\rm{ khi }}x \le 2} \end{array}} \right.$. Tính tích phân $I=\int\limits_{0}^{\sqrt{3}}{\frac{x.f\left( \sqrt{{{x}^{2}}+1} \right)}{\sqrt{{{x}^{2}}+1}}}dx+\int\limits_{\ln 2}^{\ln 3}{{{e}^{2x}}.f\left( 1+{{e}^{2x}} \right)dx}$

Câu 35:

Cho hàm số $f(x) = \left\{ {\begin{array}{*{20}{l}} {{x^2} - x}&{{\rm{ khi }}x \ge 0}\\ x&{{\rm{ khi }}x < 0} \end{array}} \right.$. Khi đó $I=2\int\limits_{0}^{\frac{\pi }{2}}{\cos xf\left( \sin x \right)}dx+2\int\limits_{0}^{2}{f\left( 3-2x \right)}dx$ bằng

Câu 36:

Cho hàm số $f(x) = \left\{ \begin{array}{l} 2{x^2} - 1\,\,\,\,\,\,{\rm{khi}}\,\,x < 0\\ x - 1\,\,\,\,\,\,\,\,\,\,\,{\rm{khi}}\,\,0 \le x \le 2\\ 5 - 2x\,\,\,\,\,\,\,\,{\rm{khi}}\,\,x > 2\, \end{array} \right.$. Tính tích phân $\int\limits_{-\frac{\pi }{4}}^{\frac{\pi }{4}}{f\left( 2-7\tan x \right)}\frac{1}{{{\cos }^{2}}x}\text{d}x$.

Câu 37:

Cho hàm số $f(x) = \left\{ \begin{array}{l} {x^4} + 2{x^2} - 1\,\,\,\,\,{\rm{khi }}x < 1\\ 3 - {x^2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm{khi }}x \ge 1 \end{array} \right.$. Tính tích phân $\int\limits_{1}^{{{e}^{4}}}{f\left( \sqrt{4-\ln x} \right)}\frac{1}{x}\text{d}x$.

Câu 38:

Cho hàm số $f(x) = \left\{ \begin{array}{l} 2x - 4\,\,\,{\rm{khi}}\,x \ge 2\\ 4 - 2x\,\,\,{\rm{khi}}\,x < 2 \end{array} \right.$. Tính tích phân $\int\limits_{-\frac{\pi }{4}}^{\frac{\pi }{2}}{f\left( 3-4{{\cos }^{2}}x \right)}\sin 2x\text{d}x$.

Câu 39:

Cho hàm số $f(x) = \left\{ \begin{array}{l} 2x - 1\,\,\,{\rm{khi}}\,x \ge 1\\ {x^2}\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm{khi}}\,x < 1 \end{array} \right.$. Tính tích phân $\int\limits_{1}^{13}{f\left( \sqrt{x+3}-2 \right)}\text{d}x$.

Câu 40:

Cho hàm số $f(x) = \left\{ \begin{array}{l} {x^3} + x + 2\,\,\,{\rm{khi }}x < 1\\ x + 3\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm{khi }}x \ge 1 \end{array} \right.$. Tính tích phân $\int\limits_{0}^{\frac{\pi }{2}}{f\left( 3{{\sin }^{2}}x-1 \right)}\sin 2x\text{d}x$.

Câu 41:

Cho hai hàm $f(x)$ và $g(x)$ có đạo hàm trên $\left[ 1;2 \right]$ thỏa mãn $f(1)=g(1)=0$ và $\left\{ \begin{array}{l} \frac{x}{{{{(x + 1)}^2}}}g(x) + 2017x = (x + 1)f'(x)\\ \frac{{{x^3}}}{{x + 1}}g'(x) + f(x) = 2018{x^2} \end{array} \right.{\rm{, }}\forall x \in \left[ {1;2} \right].$.Tính tích phân$I=\int\limits_{1}^{2}{\left[ \frac{x}{x+1}g(x)-\frac{x+1}{x}f(x) \right]}dx$.

Câu 42:

Cho hai hàm $f\left( x \right)$ và  $g\left( x \right)$ có đạo hàm trên $\left[ 1;4 \right]$, thỏa mãn $\left\{ {\begin{array}{*{20}{c}} {f\left( 1 \right) + g\left( 1 \right) = 4}\\ {g\left( x \right) = - xf'\left( x \right)}\\ {f\left( x \right) = - xg'\left( x \right)} \end{array}} \right.$ với mọi $x\in \left[ 1;4 \right]$ . Tính tích phân $I=\int\limits_{1}^{4}{\left[ f\left( x \right)+g\left( x \right) \right]dx}$.

Câu 43:

Cho hàm số $f\left( x \right)$ xác định và liên tục trên $\mathbb{R}$ đồng thời thỏa mãn $\left\{ \begin{array}{l} f\left( x \right) > 0,{\kern 1pt} \;\forall x \in R\\ f'\left( x \right) = - {e^x}{f^2}\left( x \right),{\kern 1pt} \;\forall x \in R\\ f\left( 0 \right) = \frac{1}{2} \end{array} \right..$

Tính giá trị của $f\left( \ln 2 \right)$.

Câu 44:

Cho hàm số $f(x)$ xác định trên $\mathbb{R}\backslash \left\{ -2;1 \right\}$ thỏa mãn ${f}'\left( x \right)=\frac{1}{{{x}^{2}}+x-2},f\left( -3 \right)-f\left( 3 \right)=0,f\left( 0 \right)=\frac{1}{3}$. Giá trị của biểu thức $f\left( -4 \right)+f\left( 1 \right)-f\left( 4 \right)$ bằng

Câu 45:

Xét hàm số $f\left( x \right)$ có đạo hàm liên tục trên $\mathbb{R}$ và thỏa mãn điều kiện $f\left( 1 \right)=1$ và $f\left( 2 \right)=4$. Tính $J=\int\limits_{1}^{2}{\left( \frac{{f}'\left( x \right)+2}{x}-\frac{f\left( x \right)+1}{{{x}^{2}}} \right)\text{d}x}$.

Câu 46:

Cho hàm số $f\left( x \right)$ có đạo hàm liên tục trên $\left[ 0;1 \right]$ thỏa mãn $f\left( 1 \right)=0$, $\int\limits_{0}^{1}{{{\left[ {f}'\left( x \right) \right]}^{2}}\text{d}x=7}$ và $\int\limits_{0}^{1}{{{x}^{2}}f\left( x \right)\text{d}x=\frac{1}{3}}$. Tích  phân $\int\limits_{0}^{1}{f\left( x \right)\text{d}x}$ bằng

Câu 47:

Cho hàm số $y=f\left( x \right)$ có đạo hàm trên $\mathbb{R}$ thỏa mãn $\left\{ \begin{array}{l} f\left( 0 \right) = f'\left( 0 \right) = 1\\ f\left( {x + y} \right) = f\left( x \right) + f\left( y \right) + 3xy\left( {x + y} \right) - 1 \end{array} \right.$, với $x,y\in \mathbb{R}$. Tính $\int\limits_{0}^{1}{f\left( x-1 \right)}\text{d}x$.

Câu 48:

Cho hàm số $y=f\left( x \right)$ liên tục trên $\mathbb{R}\backslash \left\{ 0;\,\,-1 \right\}$ thỏa mãn $\left\{ \begin{array}{l} f\left( 1 \right) = - 2\ln 2\\ f\left( 2 \right) = a + b\ln 3;\,\,a,\,b \in Q\\ x\left( {x + 1} \right).f'\left( x \right) + f\left( x \right) = {x^2} + x \end{array} \right.$.

Tính ${{a}^{2}}+{{b}^{2}}$.

Câu 49:

Tính tích phân $I=\int\limits_{0}^{2}{\max \left\{ {{x}^{3}},x \right\}}\text{d}x$.

Câu 50:

Giá trị của tích phân $\int\limits_{0}^{\frac{\pi }{2}}{\text{max}\left\{ \sin x,\cos x \right\}\text{d}x}$ bằng