Đề thi chính thức Tốt nghiệp THPT môn Toán năm 2025 - Đề 5
22 câu hỏi 60 phút
Trong không gian với hệ tọa độ \(Oxyz\), mặt phẳng đi qua gốc tọa độ và nhận \(\vec{n}=\left( -1;0;3 \right)\) làm một vectơ pháp tuyến có phương trình tổng quát là
\(-x-3z=0\)
\(-x+3y=0\)
\(-x+3z=0\)
\(-y+3z=0\)
Mặt phẳng đi qua gốc tọa độ và có vectơ pháp tuyến \(\vec{n}=(-1;0;3)\) có phương trình dạng \(Ax+By+Cz=0\).
Thay \(A=-1,B=0,C=3\) vào, ta được phương trình: \(-x+3z=0\).
Vậy, phương trình mặt phẳng là \(x+3z=0\).
Danh sách câu hỏi:
Mặt phẳng đi qua gốc tọa độ và có vectơ pháp tuyến \(\vec{n}=(-1;0;3)\) có phương trình dạng \(Ax+By+Cz=0\).
Thay \(A=-1,B=0,C=3\) vào, ta được phương trình: \(-x+3z=0\).
Vậy, phương trình mặt phẳng là \(x+3z=0\).
Phương trình \(\sin x=1\) có nghiệm khi \(x=\frac{\pi }{2}+k2\pi \), với \(k\in \mathbb{Z}\).
Do đó, tập nghiệm của phương trình là \(S=\left\{ \frac{\pi }{2}+k2\pi \mid k\in \mathbb{Z} \right\}\).
Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y=f(x)\), trục hoành và hai đường thẳng \(x=a\) và \(x=b\) là: \(S=\int_{a}^{b}{|}f(x)|dx\).
Trong bài này, \(f(x)=2x+1,a=1,b=2\).
Vì \(2x+1>0\) trên \([1,2]\), ta có: \(S=\int_{1}^{2}{(2x+1)}dx\).
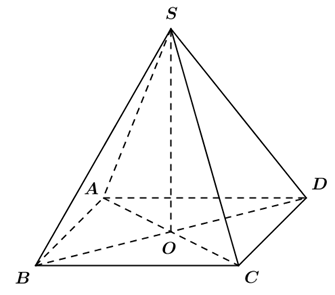
Vì \(O\) là trung điểm của \(AC\) và \(BD\), ta có \(\overrightarrow{SA}+\overrightarrow{{SC}}=2\overrightarrow{{SO}}\) và \(\overrightarrow{{SB}}+\overrightarrow{{SD}}=2\overrightarrow{{SO}}\).
Do đó, \(\overrightarrow{{SA}}+\overrightarrow{{SB}}+\overrightarrow{{SC}}+\overrightarrow{{SD}}=4\overrightarrow{{SO}}\).
\(\begin{array}{*{35}{l}} {} & {{2}^{2x+1}} & =8 \\ \Leftrightarrow & {{2}^{2x+1}} & =8 \\ \Leftrightarrow & 2x+1 & =3 \\ \Leftrightarrow & x & =1 \\\end{array}\)
Câu 13:
Một phần mềm nhận dạng tin nhắn quảng cáo trên điện thoại bằng cách dựa theo từ khóa để đánh dấu một số tin nhắn được gửi đến. Qua một thời gian dài sử dụng, người ta thấy rằng trong số tất cả các tin nhắn gửi đến, có \(20\%\) số tin nhắn bị đánh dấu. Trong số các tin nhắn bị đánh dấu, có \(10\%\) số tin nhắn không phải là quảng cáo. Trong số các tin nhắn không bị đánh dấu, có \(10\%\) số tin nhắn là quảng cáo.
Chọn ngẫu nhiên một tin nhắn được gửi đến điện thoại
Xác suất để tin nhắn đó không bị đánh dấu bằng \(0,8\)
Xác suất để tin nhắn đó không phải là quảng cáo, biết rằng nó không bị đánh dấu, bằng \(0,95\)
Xác suất để tin nhắn đó không phải là quảng cáo bằng \(0,76\)
Xác suất để tin nhắn đó không bị đánh đấu, biết rằng nó không phải là quảng cáo, nhỏ hơn \(0,95\)
Câu 14:
Cho hàm số \(f\left( x \right)={{x}^{3}}-27x+81\)
Hàm số đã cho có đạo hàm là \({f}'\left( x \right)=3{{x}^{2}}-27\)
Phương trình \({f}'\left( x \right)=0\) có tập nghiệm là \(S=\left\{ 3 \right\}\)
\(f\left( 3 \right)=27\)
Giá trị nhỏ nhất của hàm số \(f\left( x \right)\) trên đoạn \(\left[ -4;4 \right]\) bằng 27
Câu 15:
Đối với ngành nuôi trồng thủy sản, việc kiểm soát lượng thuốc tồn dư trong nước là một nhiệm vụ quan trọng nhằm đáp ứng các tiêu chuẩn an toàn về môi trường. Khi nghiên cứu một loại thuốc trị bệnh trong nuôi trồng thủy sản, người ta sử dụng thuốc đó một lần và theo dõi nồng độ thuốc tồn dư trong nước kể từ lúc sử dụng thuốc. Kết quả cho thấy nồng độ thuốc \(y\left( t \right)\) (đơn vị: mg/lit) tồn dư trong nước tại thời điểm \(t\) ngày \(\left( t\ge 0 \right)\) kể từ lúc sử dụng thuốc, thỏa mãn \(y\left( t \right)>0\) và \({y}'\left( t \right)=k.y\left( t \right)\) \(\left( t\ge 0 \right)\), trong đó \(k\) là hằng số khác không. Đo nồng độ thuốc tồn dư trong nước tại các thời điểm \(t=6\) (ngày); \(t=12\) (ngày) nhận được kết quả lần lượt là 2mg/lit; 1mg/lit. Cho biết \(y\left( t \right)={{e}^{g\left( t \right)}}\left( t\ge 0 \right)\)
\(g\left( t \right)=kt+C\left( t\ge 0 \right)\) với \(C\) là một hằng số xác định
\(k=-\frac{\ln 2}{6}\)
\(C=3\ln 2\)
Nồng độ thuốc tồn dư trong nước tại thời điểm \(t=20\) (ngày) kể từ lúc sử dụng thuốc lớn hơn \(0,4\) mg/lit
Câu 16:
Mô hình toán học sau đây được sử dụng trong quan sát chuyển động của một vật. Trong không gian cho hệ tọa độ \(Oxyz\) có \(\vec{i},\vec{j},\vec{k}\) lần lượt là các vectơ đơn vị trên các trục \(Ox,Oy,Oz\) và độ dài của mỗi vectơ đơn vị đó bằng 1 mét. Cho hai điểm \(A\) và \(B\), trong đó điểm \(A\) có tọa độ là \(\left( 6;6;0 \right)\). Một vật (coi như là một hạt) chuyển động thẳng với tốc độ phụ thuộc thời gian \(t\) (giây) theo công thức \(v\left( t \right)=\beta t+300\) (m/giây), trong đó \(\beta \) là hằng số dương và \(0\le t\le 6\). Ở thời điểm ban đầu \(\left( t=0 \right)\), vật đi qua \(A\) với tốc độ \(300\) m/giây và hướng tới \(B\). Sau \(2\) giây kể từ thời điểm ban đầu, vật đi được quãng đường \(608~m\). Gọi \(\vec{u}=\left( a;b;c \right)\) là vectơ cùng hướng với vectơ \(\overrightarrow{AB}\). Biết rằng \(\left| {\vec{u}} \right|=1\) và góc giữa vectơ \(\vec{u}\) lần lượt với các vectơ \(\vec{i},\vec{j},\vec{k}\) có số đo tương ứng bằng \({{60}^{\circ }},{{60}^{\circ }},{{45}^{\circ }}\)
\(a=\cos {{60}^{\circ }}\)
Phương trình đường thẳng \(AB\) là \(\frac{x-6}{1}=\frac{y-6}{1}=\frac{z}{2}\)
\(\beta =3\)
Giả sử sau 5 giây kể từ thời điểm ban đầu, vật đến điểm \(B\left( {{x}_{B}};{{y}_{B}};{{z}_{B}} \right)\). Khi đó \({{x}_{B}}=781\)