Đề thi thử Tốt nghiệp THPT năm 2025 môn Toán Sở GD&ĐT TP. Cần Thơ - Đề 1
22 câu hỏi 60 phút
Nguyên hàm của hàm số \(f\left( x \right)={{3}^{x}}\) là:
\(\frac{{{3}^{x}}}{\ln 3}+C\)
\({{3}^{x}}\ln 3+C\)
\({{3}^{x}}+C\)
\(\frac{{{3}^{x+1}}}{x+1}+C\)
Nguyên hàm của hàm số \(f\left( x \right)={{3}^{x}}\) là \(\frac{{{3}^{x}}}{\ln 3}+C\).
Danh sách câu hỏi:
Nguyên hàm của hàm số \(f\left( x \right)={{3}^{x}}\) là \(\frac{{{3}^{x}}}{\ln 3}+C\).
Diện tích hình phẳng giới hạn bởi đồ thị hai hàm số \(y=f\left( x \right)\), \(y=g\left( x \right)\) và hai đường thẳng \(x~=~a\), \(x~=~b\) là: \(S=\mathop{\int }_{a}^{b}\left| f\left( x \right)-g\left( x \right) \right|dx\).
Mẫu số liệu ghép nhóm có cỡ mẫu \(n=3+8+7+12+7+1+1=39\).
Gọi \({{x}_{1}},{{x}_{2}},....,{{x}_{39}}\) là điểm của 39 học sinh và giả sử dãy này đã được sắp xếp theo thứ tự tăng dần.
Tứ phân vị thứ nhất \({{Q}_{1}}\) của mẫu số liệu gốc là \(\frac{{{x}_{10}}+{{x}_{11}}}{2}\).
Do \({{x}_{10}},{{x}_{11}}\) đều thuộc nhóm \(\left[ 4;5 \right)\) nên nhóm này chứa \({{Q}_{1}}\).
Ta có \({{Q}_{1}}=4+\frac{\frac{39}{4}-3}{8}.1=\frac{155}{32}\approx 4,84\).
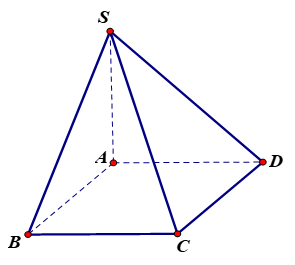
Phương trình của đường thẳng đi qua điểm \(M\left( 2;0;-1 \right)\) và có một vectơ chỉ phương \(\overrightarrow{a}=\left( 4;-6;2 \right)\) là: \(\left\{ \begin{align} & x=2+2t \\ & y=-3t \\ & z=-1+t \\ \end{align} \right.\).
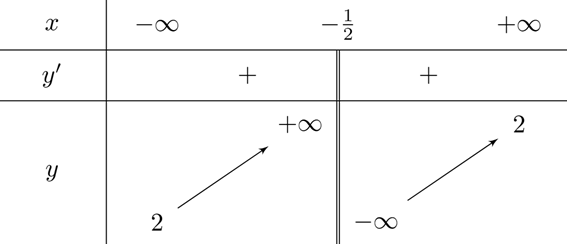
Tiệm cận ngang của đồ thị hàm số là đường thẳng có phương trình: \(y=2\).
Câu 13:
Cho hàm số \(f\left( x \right)=x-\sin 2x\)
\(f(0)=0;\,\ f(\pi )=\pi \)
Đạo hàm của hàm số đã cho là \({{f}^{'}}\left( x \right)=1+2\cos 2x\)
Nghiệm của phương trình \({{f}^{'}}\left( x \right)=0\) trên đoạn \(\left[ 0;\pi \right]\) là \(\frac{\pi }{6}\) và \(\frac{5\pi }{6}\)
Giá trị nhỏ nhất của hàm số đã cho trên đoạn \(\left[ 0;\pi \right]\) là \(\frac{\pi }{6}-\frac{\sqrt{3}}{2}\)
Câu 14:
Một nhà sản xuất trung bình bán được 1000 ti vi màn hình phẳng mỗi tuần với giá 14 triệu đồng một chiếc. Một cuộc khảo sát thị trường chỉ ra rằng nếu cứ giảm giá bán 500 nghìn đồng, số lượng ti vi bán ra sẽ tăng thêm khoảng 100 ti vi mỗi tuần. Gọi \(x\) là số ti vi bán được mỗi tuần, \(p\) (triệu đồng) là giá bán của mỗi ti vi. Khi đó \(p=p\left( x \right)\) được gọi là hàm cầu
Hàm cầu là \(p=-\frac{1}{200}x+19\) (triệu đồng)
Tổng doanh thu từ tiền bán ti vi là \(200{{p}^{2}}+3800p\) (triệu đồng)
Công ty giảm giá 4,5 triệu đồng cho người mua thì doanh thu của công ty sẽ lớn nhất
Nếu hàm chi phí hằng tuần là \(C\left( x \right)=120003x\) (triệu đồng), trong đó \(x\) là số ti vi bán ra trong tuần, nhà sản xuất nên đặt giá bán 8 triệu đồng thì lợi nhuận là lớn nhất
Câu 15:
Một xưởng máy sử dụng một loại linh kiện được sản xuất từ hai cơ sở I và II. Số linh kiện do cơ sở I sản xuất chiếm \(61\%\), số linh kiện do cơ sở II sản xuất chiếm \(39\%\). Tỉ lệ linh kiện đạt tiêu chuẩn của cơ sở I, cơ sở II lần lượt là \(93\%, 82\%\). Kiểm tra ngẫu nhiên một linh kiện ở xưởng máy. Xét các biến cố:
\({{A}_{1}}\): “Linh kiện được kiểm tra do cơ sở I sản xuất”;
\({{A}_{2}}\): “Linh kiện được kiểm tra do cơ sở II sản xuất”;
\(B\): “Linh kiện được kiểm tra đạt tiêu chuẩn”
Xác suất \(P\left( {{A}_{1}} \right)=0,61.\)
Xác suất có điều kiện \(P\left( B| {{A}_{2}} \right)=0,82.\)
Xác suất \(P\left( B \right)=0,8871.\)
Xác suất có điều kiện \(P\left( {{A}_{1}}|B \right)=0,55.\)
Câu 16:
Trong không gian \(Oxyz\) (đơn vị trên mỗi trục tính theo mét), một ngọn hải đăng được đặt ở vị trí \(I\left( 17;20;45 \right)\). Biết rằng ngọn hải đăng đó được thiết kế với bán kính phủ sáng là \(4km\)
Phương trình mặt cầu để mô tả ranh giới bên ngoài của vùng phủ sáng trên biển của hải đăng là:
\({{(x-17)}^{2}}+{{(y-20)}^{2}}+{{(z-45)}^{2}}=16000000\)
Nếu người đi biển ở vị trí \(M\left( 18;21;50 \right)\) thì không thể nhìn thấy được ánh sáng từ ngọn hải đăng
Nếu người đi biển ở vị trí \(N(4019;21;44)\) thì có thể nhìn thấy được ánh sáng từ ngọn hải đăng
Nếu hai người đi biển ở vị trí có thể nhìn thấy được ánh sáng từ ngọn hải đăng thì khoảng cách giữa hai người đó không quá \(8\) km