Đề thi thử Tốt nghiệp THPT năm 2025 môn Toán Sở GD&ĐT TP. Cần Thơ - Đề 4
22 câu hỏi 60 phút
Nguyên hàm của hàm số \(y={{2}^{x}}\) là:
\(\int{{{2}^{x}}\text{d}x=\ln {{2.2}^{x}}+C}\)
\(\int{{{2}^{x}}\text{d}x={{2}^{x}}+C}\)
\(\int{{{2}^{x}}\text{d}x=\frac{{{2}^{x}}}{\ln 2}+C}\)
\(\int{{{2}^{x}}\text{d}x=\frac{{{2}^{x}}}{x+1}+C}\)
Do theo bảng nguyên hàm: \(\int{{{a}^{x}}\text{d}x=\frac{{{a}^{x}}}{\ln \,a}+C}\).
Danh sách câu hỏi:
Do theo bảng nguyên hàm: \(\int{{{a}^{x}}\text{d}x=\frac{{{a}^{x}}}{\ln \,a}+C}\).
Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y=f\left( x \right)\), trục hoành và hai đường thẳng \(x=a,\,\,x=b\) được tính bởi công thức: \(S=\int\limits_{a}^{b}{\left| f\left( x \right) \right|}\,\text{d}x\).
Bảng tần số ghép nhóm theo giá trị đại diện là:
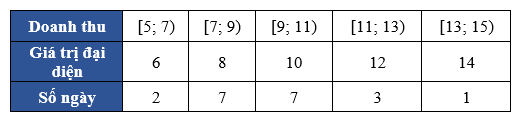
Số trung bình: \(\overline{x}=\frac{2.6\text{ }+\text{ }7.8\text{ }+\text{ }7.10\text{ }+\text{ }3.12\text{ }+\text{ }1.14}{20}=9,4\)
Ta có \(\overrightarrow{MN}=\left( 2;-1;-3 \right)\).
Đường thẳng \(MN\) đi qua điểm \(M\left( 1\,;\,2;1 \right)\) và nhận véc-tơ \(\overrightarrow{MN}=\left( 2;-1;-3 \right)\) làm véc-tơ chỉ phương có phương trình là:
\(\frac{x-1}{2}=\frac{y-2}{-1}=\frac{z-1}{-3}\).
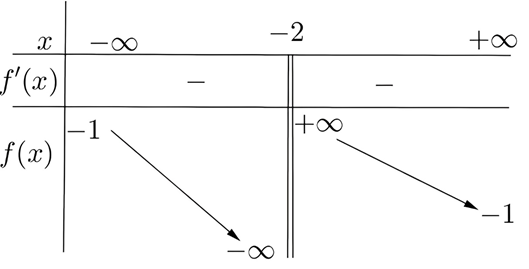
Ta thấy: \(\underset{x\to -{{2}^{+}}}{\mathop{\lim }}\,f\left( x \right)=+\infty \) và \(\underset{x\to -{{2}^{-}}}{\mathop{\lim }}\,f\left( x \right)=-\infty \).
Vậy tiệm cận đứng của hàm số đã cho là \(x=-2\).
Câu 13:
Cho hàm số \(f\left( x \right)=\sin 2x-x\)
\(f\left( -\frac{\pi }{2} \right)=\frac{\pi }{2};f\left( \frac{\pi }{2} \right)=-\frac{\pi }{2}\)
Đạo hàm của hàm số đã cho là \({f}'\left( x \right)=\cos 2x-1\)
Nghiệm của phương trình \({f}'\left( x \right)=0\) trên đoạn \(\left[ -\frac{\pi }{2};\frac{\text{ }\!\!\pi\!\!\text{ }}{2} \right]\) là \(-\frac{\pi }{6}\) hoặc \(\frac{\pi }{6}\)
Giá trị nhỏ nhất của \(f\left( x \right)\) trên đoạn \(\left[ -\frac{\pi }{2};\frac{\text{ }\!\!\pi\!\!\text{ }}{2} \right]\) là \(-\frac{\pi }{2}\)
Câu 14:
Một ô tô bắt đầu chuyển động thẳng nhanh dần đều với tốc độ \(v\left( t \right)=5t\ \ (\text{m/s});\)trong đó \(t\) là thời gian tính bằng giây kể từ khi ô tô bắt đầu chuyển động. Đi được 6(s) người lái xe phát hiện chướng ngại vật và phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với gia tốc \(a=-\,5\ (\text{m/}{{\text{s}}^{2}})\)
Tốc độ của ô tô tại thời điểm 10(s) tính từ lúc xuất phát là 10\((\text{m/s})\)
Quãng đường ô tô chuyển động được trong 6 giây đầu tiên là \(80\ \text{m}\)
Quãng đường \(S\) (đơn vị: mét) mà ô tô chuyển động được kể từ lúc bắt đầu đạp phanh đến khi dừng lại được tính theo công thức \(S=\int_{0}^{6}{(30-5t)}dt\)
Quãng đường ô tô chuyển động được kể từ lúc bắt đầu chuyển động cho đến khi dừng lại là \(170\,\text{m}\text{.}\)
Câu 15:
Một công ty đấu thầu 2 dự án. Khả năng thắng thầu của dự án 1 là \(0,4\) và khả năng thắng thầu của dự án 2 là \(0,5\). Khả năng thắng thầu cả 2 dự án là \(0,3\).
Gọi \(A\) là biến cố: “Thắng thầu dự án 1”
Gọi \(B\) là biến cố: “Thắng thầu dự án 2”.
Khi đó:
\(A\) và \(B\) là hai biến cố độc lập
Xác suất để công ty thắng thầu đúng 1 dự án bằng \(0,7\)
Xác suất để công ty thắng thầu dự án 2 biết công ty thắng thầu dự án 1 là \(0,75\)
Xác suất để công ty thắng thầu dự án 2 biết công ty không thắng thầu dự án 1 là \(0,25.\)
Câu 16:
Trong không gian với hệ tọa độ Oxyz, một cabin cáp treo xuất phát từ điểm \(A\left( 10;~3;0 \right)\) và chuyển động đều theo đường cáp có véc tơ chỉ phương \(\vec{u}=\left( 2;-2;1 \right)\) (hướng chuyển động cùng chiều với hướng véc tơ \(\vec{u}\) với tốc độ là \(4,5\ (\text{m/s});\) (đơn vị trên mỗi trục là mét)
Phương trình tham số của đường cáp là: \(\left\{ \begin{align} & x=10+2t \\ & y=3-2t \\ & z=t \\ \end{align} \right.\text{, }\left( t\in \mathbb{R} \right)\)
Giả sử sau thời gian t (s) kể từ khi xuất phát (\(t\ge 0\)), cabin đến điểm M. Khi đó tọa độ điểm M là \(M(3t+10;~-3t+3;~\frac{3t}{2}\) )
Cabin dừng ở điểm B có hoành độ \({{x}_{B}}=550\), khi đó quãng đường AB dài 800m
Đường cáp AB tạo với mặt phẳng (Oxyz) một góc \({{30}^{o}}\)