Đề thi thử Tốt nghiệp THPT năm 2025 môn Toán cụm trường miền Bắc - Đề 1
22 câu hỏi 60 phút
Trên đoạn \(\left[ 0;3 \right]\), hàm số \(y=-{{x}^{3}}+3x\) đạt giá trị nhỏ nhất tại điểm?
\(x=0\)
\(x=3\)
\(x=1\)
\(x=2\)
Ta có \(y'=-3{{x}^{2}}+3=0\Leftrightarrow \left[ \begin{align} & x=-1\notin \left( 0;3 \right) \\ & x=1\in \left( 0;3 \right) \\ \end{align} \right.\)
Ta có: \(y(0)=0,\,y(1)=2,\,y(3)=-18\).
Vậy hàm số đạt giá trị nhỏ nhất tại \(x=3\).
Danh sách câu hỏi:
Ta có \(y'=-3{{x}^{2}}+3=0\Leftrightarrow \left[ \begin{align} & x=-1\notin \left( 0;3 \right) \\ & x=1\in \left( 0;3 \right) \\ \end{align} \right.\)
Ta có: \(y(0)=0,\,y(1)=2,\,y(3)=-18\).
Vậy hàm số đạt giá trị nhỏ nhất tại \(x=3\).
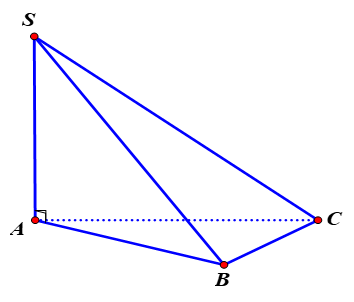
Ta có \(\left\{ \begin{align} & \left( SAB \right)\cap \left( SAC \right)=SA \\ & AB\bot SA \\ & AC\bot SA \\ \end{align} \right.\)
Do đó góc giữa hai mặt phẳng \((SAB)\) và \((SAC)\) là góc giữa hai đường thẳng\(AB\) và \(AC\).
Xét tam giác \(ABC\) có: \(\cos A=\frac{A{{B}^{2}}+A{{C}^{2}}-B{{C}^{2}}}{2AB.AC}=\frac{{{a}^{2}}+{{a}^{2}}-3{{a}^{2}}}{2{{a}^{2}}}=-\frac{1}{2}\), do đó \(\widehat{BAC}=120{}^\circ \).
Suy ra góc giữa \(AB\) và \(AC\) bằng \(180{}^\circ -120{}^\circ =60{}^\circ \).
Vậy góc giữa hai mặt phẳng \((SAB)\) và \((SAC)\) là \(60{}^\circ \).
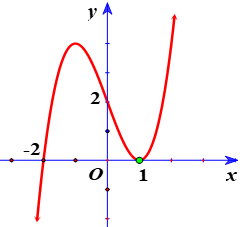
Vì đồ thị hàm số \(y={{(x-1)}^{2}}(x+2)\) cắt \(Ox\) tại điểm có hoành độ \(-2\) và tiếp xúc \(Ox\) tại điểm có hoành độ \(1\).
Yêu cầu đề bài tương đương với tìm điều kiện của \({{x}_{0}}\) để \({{\log }_{3}}{{x}_{0}}>2\Leftrightarrow {{x}_{0}}>9\).
Số cách lấy 1 quyển sách Toán và 1 quyển sách Văn là: \(6.7=42\) cách.
Số cách lấy 1 quyển sách Toán và 1 quyển sách Tiếng Anh là: \(6.8=48\) cách.
Số cách lấy 1 quyển sách Tiếng Anh và 1 quyển sách Văn là: \(8.7=56\) cách.
Vậy theo quy tắc cộng ta có \(42+48+56=146\) cách.
Câu 13:
Cho hình hộp \(ABCD.{A}'{B}'{C}'{D}'\). Các điểm \(M,\,\,N\) lần lượt thuộc các đường thẳng \(CA\) và \(D{C}'\) sao cho \(\overrightarrow{MC}=m\overrightarrow{MA};\,\,\overrightarrow{ND}=m\overrightarrow{N{C}'}\) trong đó tham số \(m\ne 1\). Đặt \(\overrightarrow{BA}=\overrightarrow{a};\,\,\overrightarrow{B{B}'}=\overrightarrow{b};\,\,\overrightarrow{BC}=\overrightarrow{c}\)
\(\overrightarrow{B{D}'}=\overrightarrow{a}+\overrightarrow{b}-\overrightarrow{c}\)
\(\overrightarrow{BM}=\frac{\vec{c}-m\vec{a}}{1-m}\)
\(\overrightarrow{BN}=\frac{1}{1-m}\overrightarrow{a}-\frac{m}{1-m}\vec{b}+\overrightarrow{c}\)
Khi \(m=\frac{1}{2}\) thì \(MN\,\parallel \,B{D}'\)
Câu 14:
Giả sử số lượng của một quần thể nấm men tại môi trường nuôi cấy trong phòng thí nghiệm được mô hình hóa bằng hàm số \(P\left( t \right)=\frac{a}{b+{{e}^{-\frac{3}{4}t}}}\), trong đó thời gian \(t\) được tính bằng giờ và \(a,b\in \mathbb{R}\). Tại thời điểm ban đầu \(t=0\), quần thể có \(20\) tế bào và tăng tốc với tốc độ \(12\) tế bào/giờ
Độ tăng tốc của quần thể nấm men được tính theo hàm số \({P}'\left( t \right)=\frac{\frac{3}{4}a.{{e}^{-\frac{3}{4}t}}}{{{\left( b+{{e}^{-\frac{3}{4}t}} \right)}^{2}}}\)
\(P\left( 0 \right)=20\) và \({P}'\left( 0 \right)=12\)
Về lâu dài, lượng quần thể nấm men luôn tăng
Về lâu dài, số lượng nấm men của quần thể sẽ vượt quá \(100\) tế bào
Câu 15:
Giả sử chi phí mua và bảo trì một thiết bị trong \(x\) năm có thể được mô hình hóa theo công thức \(C=5000\left( 25+3\int\limits_{0}^{x}{{{t}^{\frac{1}{4}}}dt} \right)\). Khi ấy:
Chi phí mua 1 sản phẩm là 100.000 đồng
Chi phí bảo trì năm đầu tiên của 1 sản phẩm là 12.000 đồng
Sau 6,5 năm thì số tiền mua một sản phẩm bằng số tiền bảo trì sản phẩm đó
Nếu một nhà đầu tư có 10 triệu, thì họ có thể mua và bảo trì tối đa 30 sản phẩm trong 10 năm
Câu 16:
Để thành lập đội tuyển quốc gia môn tin học, người ta tổ chức một cuộc thi tuyển gồm 3 vòng. Vòng thứ nhất lấy 60% thí sinh dự thi, vòng thứ hai lấy 20% thí sinh đã qua vòng thứ nhất và vòng thứ ba lấy 10% thí sinh đã qua vòng thứ hai. Để vào được đội tuyển, thí sinh phải vượt qua được cả ba vòng thi. Xác suất một thí sinh dự thi bất kì:
“Bị loại ở vòng thứ nhất” là 40%
“Được vào đội tuyển quốc gia” là 1,2%
”Vượt qua vòng 1 và 2 nhưng bị loại ở vòng thứ 3” là 10,8%
“Bị loại ở vòng thứ 2, biết rằng thí sinh này bị loại” là khoảng 48,58%