Trong không gian \(Oxyz\), cho hai vectơ \(\overrightarrow{u}\left( 1;3;-2 \right)\) và \(\overrightarrow{v}\left( 2;1;-1 \right)\). Tọa độ của \(\overrightarrow{u}-\overrightarrow{v}\) là:

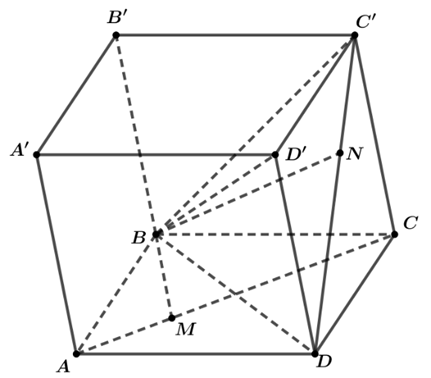
a) Sai.

Ta có \(\overrightarrow{B{D}'}=\overrightarrow{B{B}'}+\overrightarrow{BA}+\overrightarrow{BC}=\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}\).

b) Đúng.

Ta có:

\(\overrightarrow{BM}=\overrightarrow{BC}+\overrightarrow{CM}=\overrightarrow{BC}-\overrightarrow{MC}=\overrightarrow{BC}-m\overrightarrow{MA}=\overrightarrow{BC}-m\left( \overrightarrow{MB}+\overrightarrow{BA} \right)\)

\(\Rightarrow \overrightarrow{BM}=\overrightarrow{BC}+m\overrightarrow{BM}-m\overrightarrow{BA}\)

\(\Leftrightarrow \overrightarrow{BM}-m\overrightarrow{BM}=\overrightarrow{BC}-m\overrightarrow{BA}\)

\(\Leftrightarrow \left( 1-m \right)\overrightarrow{BM}=\vec{c}-m\vec{a}\)

\(\Leftrightarrow \overrightarrow{BM}=\frac{\vec{c}-m\vec{a}}{1-m}\).

c) Đúng.

Ta có:

\(\overrightarrow{BN}=\overrightarrow{BD}+\overrightarrow{DN}=\overrightarrow{BD}-\overrightarrow{ND}=\overrightarrow{BD}-m\overrightarrow{N{C}'}=\overrightarrow{BD}-m\left( \overrightarrow{NB}+\overrightarrow{B{C}'} \right)\)

\(\Rightarrow \overrightarrow{BN}=\overrightarrow{BD}+m\overrightarrow{BN}-m\overrightarrow{B{C}'}\)

\(\Leftrightarrow \left( 1-m \right)\overrightarrow{BN}=\overrightarrow{BD}-m\overrightarrow{B{C}'}\)

\(\Leftrightarrow \overrightarrow{BN}=\frac{\overrightarrow{BD}-m\overrightarrow{B{C}'}}{1-m}\)

\(\begin{array}{*{35}{l}}   \Leftrightarrow \overrightarrow{BN} & =\frac{\left( \overrightarrow{BA}+\overrightarrow{BC} \right)-m\left( \overrightarrow{B{B}'}+\overrightarrow{BC} \right)}{1-m}  \\   {} & =\frac{\vec{a}+\vec{c}-m\left( \vec{b}+\vec{c} \right)}{1-m}  \\   {} & =\frac{1}{1-m}\vec{a}-\frac{m}{1-m}\vec{b}+\vec{c}.  \\\end{array}\)

d) Sai.

Ta có \(\overrightarrow{MN}=\overrightarrow{BN}-\overrightarrow{BM}=\frac{1+m}{1-m}\overrightarrow{a}-\frac{m}{1-m}\overrightarrow{b}-\frac{m}{1-m}\overrightarrow{c}\).

Vì \(MN//B{D}'\Leftrightarrow \overrightarrow{MN}=k\overrightarrow{B{D}'}\Leftrightarrow \overrightarrow{MN}=k\overrightarrow{a}+k\overrightarrow{b}+k\overrightarrow{c}\).

\(\Rightarrow\left\{\begin{array}{l}\frac{1+m}{1-m}=k \\\frac{-m}{1-m}=k \Leftrightarrow\left\{\begin{array}{l}1+m=(1-m) k \\-m=(1-m) k\end{array} \Leftrightarrow-m=1+m \Leftrightarrow m=\frac{-1}{2} .\right. \\\frac{-m}{1-m}=k\end{array}\right.\)

a) Đúng.

Ta có \(P\left( t \right)=\frac{a}{b+{{e}^{-\frac{3}{4}t}}}\).

\(\Rightarrow {P}'\left( t \right)=a.\left[ -\frac{{{\left( b+{{e}^{-\frac{3}{4}t}} \right)}^{\prime }}}{{{\left( b+{{e}^{-\frac{3}{4}t}} \right)}^{2}}} \right]=-a.\frac{{{\left( -\frac{3}{4}t \right)}^{\prime }}.{{e}^{-\frac{3}{4}t}}}{{{\left( b+{{e}^{-\frac{3}{4}t}} \right)}^{2}}}=\frac{\frac{3}{4}a.{{e}^{-\frac{3}{4}t}}}{{{\left( b+{{e}^{-\frac{3}{4}t}} \right)}^{2}}}\).

Vậy độ tăng tốc của quần thể nấm men là:

\({P}'\left( t \right)=\frac{3}{4}a.{{e}^{-\frac{3}{4}t}}.\frac{1}{{{\left( b+{{e}^{-\frac{3}{4}t}} \right)}^{2}}}\).

b) Đúng.

Tại thời điểm ban đầu \(t=0\), quần thể có \(20\) tế bào nên \(P\left( 0 \right)=20\).

Quần thể nấm men tăng tốc với tốc độ \(12\) tế bào/giờ nên \({P}'\left( 0 \right)=12\).

c) Đúng.

Ta có \(P\left( 0 \right)=20\Rightarrow \frac{a}{b+1}=20\) và \({P}'\left( 0 \right)=12\Rightarrow \frac{3}{4}a.\frac{1}{{{\left( b+1 \right)}^{2}}}=12\).

Với \(\frac{a}{b+1}=20\Rightarrow b+1=\frac{a}{20}\), khi đó \(\frac{3}{4}a.\frac{1}{{{\left( b+1 \right)}^{2}}}=12\) được viết thành:

\(\frac{\frac{3}{4}a}{{{\left( \frac{a}{20} \right)}^{2}}}=12\Rightarrow \frac{3}{4}a=12{{\left( \frac{a}{20} \right)}^{2}}\Rightarrow \frac{3}{100}{{a}^{2}}-\frac{3}{4}a=0\Rightarrow \left[ \begin{align}  & a=0\Rightarrow b=-1\,\,\,\,\left( l \right) \\  & a=25\Rightarrow b=\frac{1}{4}\,\,\,\left( n \right) \\ \end{align} \right.\)

Vậy \(a=25,b=\frac{1}{4}\).

\(\Rightarrow P\left( t \right)=\frac{25}{\frac{1}{4}+{{e}^{-\frac{3}{4}t}}}\Rightarrow {P}'\left( t \right)=\frac{75}{4}{{e}^{-\frac{3}{4}t}}.\frac{1}{{{\left( \frac{1}{4}+{{e}^{-\frac{3}{4}t}} \right)}^{2}}}>0,\forall t\ge 0\). (*)

Khi đó về lâu dài, lượng quần thể nấm men luôn tăng.

d) Sai.

Từ (*) ta có bảng biến thiên như sau:

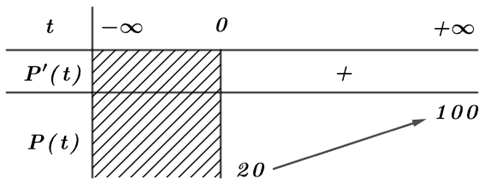
Về lâu dài, số lượng nấm men của quần thể sẽ không vượt quá \(100\) tế bào.

a) Sai.

Chi phí mua 1 sản phẩm ứng với \(x=0\), sau ra \(C=5000.25=125.000\).

b) Đúng.

Với \(x=1\) ta có \(C=5000\left( 25+3\int\limits_{0}^{1}{{{t}^{\frac{1}{4}}}dt} \right)=137.000\).

Suy ra chi phí bảo trì năm đầu tiên của sản phẩm là: \(137.000-125.000=12.000\) đồng.

c) Sai

Gọi \(x\) là số năm mà số tiền bảo trì bằng số tiền mua sản phẩm.

Khi đó tổng số tiền mua và số tiền bảo trì là \(2*125.000=250.000\).

Khi ấy ta có: 

\(\begin{align}  & 5000\left( 25+3\int\limits_{0}^{x}{{{t}^{\frac{1}{4}}}dt} \right)=250.000 \\  & \Leftrightarrow 25+3\left( \frac{4}{5}{{t}^{\frac{5}{4}}}|_{0}^{x} \right)=50 \\  & \Leftrightarrow \frac{12}{5}{{x}^{\frac{5}{4}}}=25 \\ \end{align}\)

\(\Leftrightarrow x={{\left( \frac{75}{2} \right)}^{\frac{4}{5}}}\approx 6.52\) năm.

d) Sai

Số tiền mua và bảo trì 1 sản phẩm trong 10 năm là: \(C=5000\left( 25+3\int\limits_{0}^{10}{{{t}^{\frac{1}{4}}}dt} \right)=5000\left( 25+24\sqrt[4]{10} \right)\approx 338.393,53\).

Ta có \(\frac{10.000.000}{338.393,53}\approx 29,55\).

Vậy với 10 triệu thì họ có thể mua và bảo trì tối đa 29 sản phẩm.

a) Đúng

Gọi \({{A}_{1}},{{A}_{2}},{{A}_{3}}\) lần lượt là biến cố thí sinh phải vượt qua vòng thứ nhất, thứ hai và thứ ba.

Khi ấy ta có \(P\left( {{A}_{1}} \right)=0,6\Rightarrow P\left( \overline{{{A}_{1}}} \right)=1-0,6=0,4\).

Vậy xác suất một thí sinh dự thi bất kì “Bị loại ở vòng thứ nhất” là: \(P\left( \overline{{{A}_{1}}} \right)=0,4=40%\).

b) Đúng

Xác suất để thí sinh qua vòng thứ 2, với điều kiện đã qua vòng 1 là: \(P\left( {{A}_{2}}|{{A}_{1}} \right)=0,2\).

Xác suất để thí sinh qua vòng thứ 3, với điều kiện đã qua vòng 1 và 2 là: \(P\left( {{A}_{3}}|{{A}_{1}}{{A}_{2}} \right)=0,1\).

Khi ấy ta lần lượt có:

\(P\left( \overline{{{A}_{2}}}|{{A}_{1}} \right)=1-0,2=0,8\) và \(P\left( \overline{{{A}_{3}}}|{{A}_{1}}{{A}_{2}} \right)=1-0,1=0,9\).

Với biến cố cần tìm là được vào tuyển quốc gia (tức qua được cả 3 vòng) nên ta suy ra xác suất cần tìm bằng (áp dụng công thức xác suất toàn phần).

\(\begin{align} \mathrm{P}\left(\mathrm{A}_1 \mathrm{~A}_2 \mathrm{~A}_3\right) & =\mathrm{P}\left(\mathrm{A}_3 \mid \mathrm{A}_2 \mathrm{~A}_1\right) \cdot \mathrm{P}\left(\mathrm{A}_2 \mathrm{~A}_1\right) \\ & =\mathrm{P}\left(\mathrm{A}_3 \mid \mathrm{A}_2 \mathrm{~A}_1\right) \cdot \mathrm{P}\left(\mathrm{A}_2 \mid \mathrm{A}_1\right) \cdot \mathrm{P}\left(\mathrm{A}_1\right) \\ & =0,6 \cdot 0,2 \cdot 0,1=1,2 \%\end{align}\)

c) Đúng

Xác suất một thí sinh dự thi bất kì ”Vượt qua vòng 1 và 2 nhưng bị loại ở vòng thứ 3” là: 

\(P\left( {{A}_{1}}{{A}_{2}}\overline{{{A}_{3}}} \right)=P\left( \overline{{{A}_{3}}}|{{A}_{2}}{{A}_{1}} \right).P\left( {{A}_{2}}|{{A}_{1}} \right).P\left( {{A}_{1}} \right)=0,6.0,2.0,9=10,8%\).

d) Đúng

Gọi \(X\) là biến cố thí sinh chắc chắn bị loại, khi ấy ta có \(X=\overline{{{A}_{1}}{{A}_{2}}{{A}_{3}}}\).

Xác suất một thí sinh dự thi bất kì “Bị loại ở vòng thứ 2, biết rằng thí sinh này bị loại” là:

\(\begin{align} \mathrm{P}\left(\mathrm{A}_1 \overline{\mathrm{~A}_2} \mid \mathrm{X}\right) & =\frac{\mathrm{P}\left(\mathrm{A}_1 \cdot \overline{\mathrm{~A}_2} \cdot \overline{\mathrm{~A}_1 \mathrm{~A}_2 \mathrm{~A}_3}\right)}{\mathrm{P}\left(\overline{\mathrm{A}_1 \mathrm{~A}_2 \mathrm{~A}_3}\right)} \\ & =\frac{\mathrm{P}\left(\mathrm{A}_1 \overline{\mathrm{~A}_2}\right)}{1-\mathrm{P}\left(\mathrm{A}_1 \mathrm{~A}_2 \mathrm{~A}_3\right)} \\ & =\frac{\mathrm{P}\left(\overline{\mathrm{A}_2} \mid \mathrm{A}_1\right) \cdot \mathrm{P}\left(\mathrm{A}_1\right)}{1-\mathrm{P}\left(\mathrm{A}_1 \mathrm{~A}_2 \mathrm{~A}_3\right)} \\ & =\frac{0,80,6}{1-0,012}=48,58 \%\end{align}\)

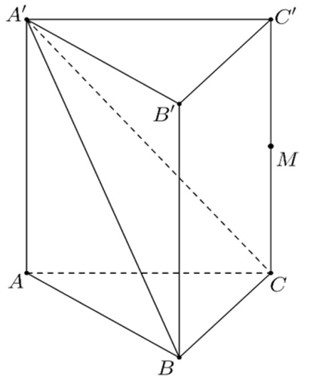
Ta có:

\(d\left( M,\left( A'BC \right) \right)=\frac{1}{2}d\left( A,\left( A'BC \right) \right)=\frac{1}{2}.\frac{3.\frac{\sqrt{3}}{2}.3}{\sqrt{{{3}^{2}}+{{\left( \frac{\sqrt{3}}{2}.3 \right)}^{2}}}}=\frac{3\sqrt{21}}{14}\).

Mặt khác, \({{S}_{A'BC}}=\frac{1}{2}.3.\frac{3\sqrt{7}}{2}=\frac{9\sqrt{7}}{4}\).

Vậy \({{V}_{M.A'BC}}=\frac{1}{3}.\frac{3\sqrt{21}}{14}.\frac{9\sqrt{7}}{4}\approx 1,9\).