Câu hỏi:
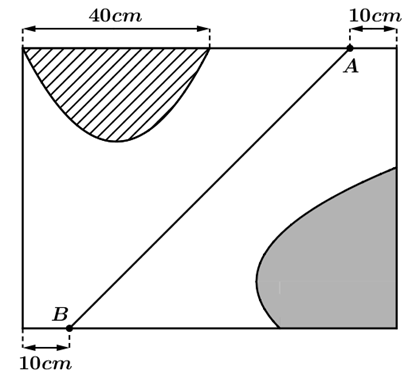
Để trang trí cửa sổ hình chữ nhật với kích thước \(80cm\times 60cm\) thì anh Duy đã tô màu 2 hoạ tiết giới hạn bởi Parabol \(f\left( x \right)\) , hàm số \(g\left( x \right)\) và các cạnh của cửa sổ bằng màu vàng (kí hiệu sọc nghiêng) và màu xanh (vùng tô đậm) (như hình vẽ). Biết rằng đồ thị hàm số của\(f\left( x \right)\) và \(g\left( x \right)\) đối xứng nhau qua đường thẳng \(AB\) và diện tích phần màu vàng bằng \(\frac{1600}{3}\left( c{{m}^{2}} \right)\). Biết mỗi lọ sơn, sơn được tối đa \(30c{{m}^{2}}\) thì tổng số tiền (đơn vị: triệu đồng và làm tròn đến phần trăm) bạn cần phải trả để trang trí cửa sổ bẳng bao nhiêu? Cho biết giá của một lọ sơn vàng là \(50.000\) đồng, giá của một lọ sơn xanh là \(30.000\) đồng (lọ sơn không bán lẻ).
Đáp án đúng: 1,68
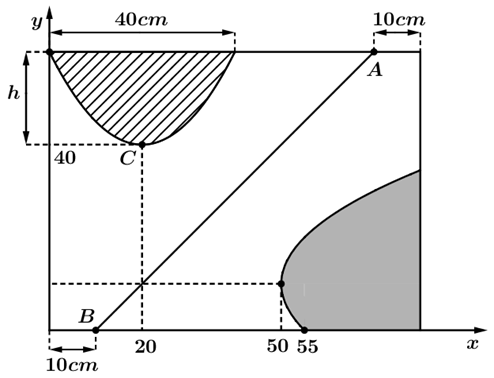
Đầu tiên ta có diện tích của phần tô vàng (tức diện tích phần kẻ sọc) là (áp dụng công thức tính nhanh diện tích parabol) ta có:
\({{S}_{v}}=\frac{2}{3}h.40=\frac{1600}{3}\to h=20\to d\left( C;Ox \right)=60-20=40\to C\left( 20;40 \right)\).
Xét parabol phần tô vàng có dạng \(\left( P \right):y=a{{x}^{2}}+bx+c\).
Biết \(\left( P \right)\cap Oy=D\left( 0;60 \right)\) và \(C\left( 20;40 \right)\in \left( P \right)\) và vừa là đỉnh là parabol, dễ dàng suy ra được \(x=20\) là trục đối xứng tức \(\left( P \right):y=a{{\left( x-20 \right)}^{2}}+40\).
Với \(C\left( 20;40 \right)\in \left( P \right)\) ta giải ra \(a=\frac{1}{20}\) tức ta có:
\(\left( P \right):y=\frac{1}{20}{{\left( x-20 \right)}^{2}}+40\).
Tiếp đến xét đường thẳng \(AB\) đi qua 2 điểm \(A\left( 10;0 \right)\) và \(B\left( 70;60 \right)\), khi ấy ta có
\(\left( AB \right):y=x-10\).
Gọi \(M\left( {{x}_{0}};{{y}_{0}} \right)\in f\left( x \right),N\left( x;y \right)\in g\left( x \right)\). Do đồ thị hàm số của \(f\left( x \right)\) và \(g\left( x \right)\) đối xứng nhau qua đường thẳng \(AB\) nên suy ra ta có hệ sau
\(\left\{\begin{array}{l}\frac{x+x_0}{2}-\frac{y+y_0}{2}-10=0 \\ \frac{x-x_0}{1}=\frac{y-y_0}{-1}\end{array} \Rightarrow\left\{\begin{array}{l}x_0=y+10 \\ y_0=x-10\end{array}\right.\right.\),
mà \(M\in \left( P \right):y=\frac{1}{20}{{\left( x-20 \right)}^{2}}+40\).
Nên khi ấy ta có:
\({{y}_{0}}=\frac{1}{20}{{\left( {{x}_{0}}-20 \right)}^{2}}+40\Rightarrow x-10=\frac{1}{20}{{\left( y+10-20 \right)}^{2}}+40\).
Suy ra
\(x=\frac{1}{20}{{\left( y-10 \right)}^{2}}+50\ge 50\to x\ge 50\to y=10\pm \sqrt{20x-1000}\).
Khi ấy phần tô xanh (phần in đậm) giới hạn bởi:
\(\left\{ \begin{align} & y=10\pm \sqrt{20x-1000} \\ & x=50,x=80 \\ \end{align} \right.\)
Suy ra diện tích là:
\({{S}_{x}}=\int\limits_{50}^{80}{\left| \sqrt{20x-1000}+10 \right|dx}+\int\limits_{50}^{55}{\left| -\sqrt{20x-1000}+10 \right|dx}\approx 773,231\left( c{{m}^{2}} \right)\).
Do mỗi lọ sơn chỉ sơn tối đa \(30c{{m}^{2}}\) nên lần lượt suy ra:
Số lọ sơn vàng là
\(\frac{{{S}_{v}}}{30}=\frac{{1600}/{3}\;}{30}\approx 17,77\) (lọ) tức cần 18 lọ sơn vàng.
Số lọ sơn xanh là
\(\frac{{{S}_{x}}}{30}=\frac{773,231}{30}\approx 25,77\) (lọ) tức cần 26 lọ sơn xanh.
Vậy số tiền cần dùng là
\(18\times 50,000+26\times 30,000=1,680,000\) (đồng) tức 1,68 triệu đồng.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Tuyển Tập Đề Thi Tham Khảo Tốt Nghiệp THPT Quốc Gia Năm 2025 - Toán - Bộ Đề 06 được biên soạn nhằm hỗ trợ học sinh ôn tập toàn diện và làm quen với cấu trúc đề thi tốt nghiệp THPT Quốc gia. Đề thi có thời gian làm bài 90 phút, bao phủ toàn bộ chương trình Toán THPT, với 75-85% nội dung thuộc chương trình lớp 12 và phần còn lại được chọn lọc từ lớp 10, 11, giúp học sinh ôn tập và củng cố kiến thức qua các năm học. Các chuyên đề trọng tâm như hàm số, đạo hàm, tích phân, phương trình bậc hai, hình học không gian, tổ hợp - xác suất, số phức và phương pháp tọa độ trong mặt phẳng đều được đưa vào trong đề thi. Cấu trúc đề thi gồm ba phần: Câu Trắc Nghiệm Nhiều Phương Án Lựa Chọn, Câu Trắc Nghiệm Đúng Sai và Câu Trắc Nghiệm Trả Lời Ngắn, giúp học sinh tiếp cận nhiều dạng bài từ cơ bản đến nâng cao. Đây là tài liệu ôn luyện hữu ích giúp học sinh phát triển tư duy toán học và tự tin đối mặt với kỳ thi tốt nghiệp THPT 2025.
Câu hỏi liên quan

Bộ 50 Đề Thi Thử Tốt Nghiệp THPT Giáo Dục Kinh Tế Và Pháp Luật Năm 2026 – Theo Cấu Trúc Đề Minh Họa Bộ GD&ĐT

Bộ 50 Đề Thi Thử Tốt Nghiệp THPT Lịch Sử Học Năm 2026 – Theo Cấu Trúc Đề Minh Họa Bộ GD&ĐT

Bộ 50 Đề Thi Thử Tốt Nghiệp THPT Công Nghệ Năm 2026 – Theo Cấu Trúc Đề Minh Họa Bộ GD&ĐT

Bộ 50 Đề Thi Thử Tốt Nghiệp THPT Môn Hóa Học Năm 2026 – Theo Cấu Trúc Đề Minh Họa Bộ GD&ĐT

Bộ 50 Đề Thi Thử Tốt Nghiệp THPT Môn Sinh Học Năm 2026 – Theo Cấu Trúc Đề Minh Họa Bộ GD&ĐT