Đề thi thử Tốt nghiệp THPT năm 2026 môn Toán Sở GD&DT TP. Hồ Chí Minh - Đề 1
22 câu hỏi 60 phút
Họ nguyên hàm của hàm số \(f\left( x \right)={{e}^{x}}+x\) là
\({{e}^{x}}+{{x}^{2}}+C\)
\({{e}^{x}}+\frac{1}{2}{{x}^{2}}+C\)
\(\frac{1}{x+1}{{e}^{x}}+\frac{1}{2}{{x}^{2}}+C\)
\({{e}^{x}}+1+C\)
Danh sách câu hỏi:
Diện tích hình phẳng giới hạn bởi các đường \(y={{\text{e}}^{x}}\), \(y=0\), \(x=0\), \(x=2\) là:
\(S=\int\limits_{0}^{2}{{{\text{e}}^{x}}}\text{d}x\).
Lĩnh vực \(A\)
Lĩnh vực \(B\)
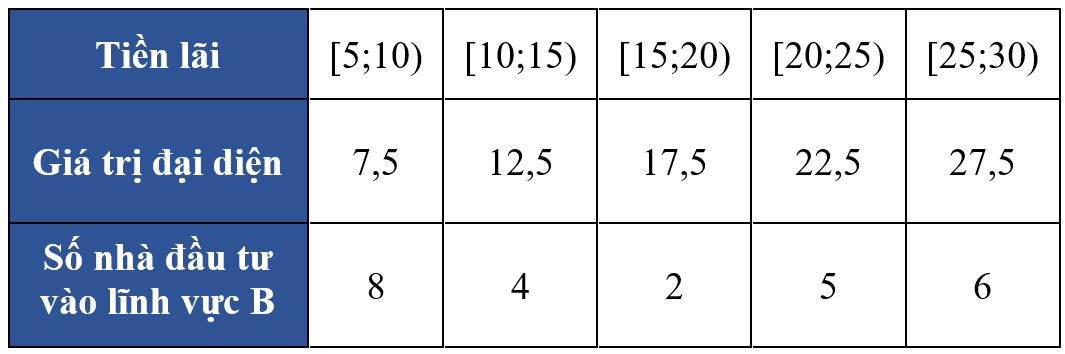
Giá trị trung bình của hai lĩnh vực \(A\) và \(B\) là.
\(\overline{{{x}_{A}}}=\frac{1}{25}\cdot \left( 2.7,5+5.12,5+8.17,5+6.22,5+4.27,5 \right)=18,5\).
\(\overline{{{x}_{B}}}=\frac{1}{25}\cdot \left( 8.7,5+4.12,5+2.17,5+5.22,5+6.27,5 \right)=16,9\).
Về độ trung bình đầu tư vào lĩnh vực \(A\) lãi hơn lĩnh vực \(B\).
Độ lệch chuẩn của hai lĩnh vực \(A\) và \(B\) là.
\({{s}_{A}}=\sqrt{\frac{1}{25}\cdot \left( 2.7,{{5}^{2}}+5.12,{{5}^{2}}+8.17,{{5}^{2}}+6.22,{{5}^{2}}+4.27,{{5}^{2}} \right)-18,{{5}^{2}}}=5,8\).
\({{s}_{B}}=\sqrt{\frac{1}{25}\cdot \left( 8\cdot 7,{{5}^{2}}+4\cdot 12,{{5}^{2}}+2\cdot 17,{{5}^{2}}+5\cdot 22,{{5}^{2}}+6\cdot 27,{{5}^{2}} \right)-16,{{9}^{2}}}=8,04\).
Như vậy độ lệch chuẩn của mẫu số liệu thu tiền được hàng tháng khi đầu tư vào lĩnh vực \(B\) cao hơn lĩnh vực \(A\) nên đầu tư vào lĩnh vực \(B\) rủi ro hơn.
Ta có \(\overrightarrow{AB}=\left( 1;-2;1 \right)\).
Đường thẳng \(AB\) đi qua điểm \(A\left( 1;1;2 \right)\) và nhận véctơ \(\overrightarrow{AB}=\left( 1;-2;1 \right)\) làm véctơ chỉ phương.
Vậy phương trình của \(AB\) là \(\frac{x-1}{1}=\frac{y-1}{-2}=\frac{z-2}{1}\).
Vì \(\underset{x\to {{(-1)}^{+}}}{\mathop{\text{lim}}}\,y=+\infty \) nên hàm số có tiệm cận đứng \(x=-1\).
Câu 8:
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi, \(SA=SC\). Khẳng định nào sau đây đúng?
Câu 13:
Cho hàm số \(f\left( x \right)={{e}^{x}}+x\)
Tính \(f\left( 0 \right)=1\) và \(f\left( \text{ln}2 \right)=2+\text{ln}2\)
Đạo hàm của hàm số đã cho là \({f}'\left( x \right)={{e}^{x}}+1\)
Nghiệm của phương trình \({f}'\left( x \right)=0\) trên đoạn \(\left[ 0;1 \right]\) là 2
Giá trị lớn nhất của \(f\left( x \right)\) trên đoạn \(\left[ 0;\text{ln}2 \right]\) là \(2+\text{ln}2\)
Câu 14:
Để đảm bảo an toàn khi khi lưu thông trên đường, các xe ô tô khi dừng đèn đỏ phải cách nhau tối thiểu 1 m. Ô tô A đang chạy với vận tốc \(16\text{m}/\text{s}\) bỗng gặp ô tô B đang dừng đèn đỏ phía trước nên ô tô A đạp phanh và chuyển động chậm dần đều với vận tốc \(v\left( t \right)=16-4t\left( \text{m}/\text{s} \right)\), trong đó \(t\) là khoảng thời gian tính bằng giây kể từ thời điểm ô tô A bắt đầu đạp phanh. Các mệnh đề sau đúng hay sai?
Ô tô A sẽ dừng lại khi vận tốc bằng 0
Ô tô A dừng lại tại thời điểm \(t=5\)
Quãng đường ô tô A đi được kể từ thời điểm bắt đầu hãm phanh đến lúc dừng lại là \(s=\int _{0}^{5}v\left( t \right)dt\)
Để hai ô tô A và B khi dừng lại đạt khoảng cách an toàn thì ô tô A phải đạp phanh khi cách ô tô B một khoảng tối thiểu là 30 mét
Câu 15:
Một chiếc hộp có \(80\) viên bi, trong đó có \(50\) viên bi màu đỏ và 30 viên bi màu vàng; các viên bi có kích thước và khối lượng như nhau. Sau khi kiểm tra, người ta thấy có \(60\) số viên bi màu đỏ đánh số và \(50\) số viên bi màu vàng có đánh số, những viên bi còn lại không đánh số. Lấy ngẫu nhiên một viên bi trong hộp. Gọi \(A\) là biến cố "Viên bi được lấy ra có đánh số", \(B\) là biến cố "Viên bi được lấy ra có màu đỏ"
Số viên bi màu đỏ có đánh số là 30
\(P\left( B \right)=\frac{3}{5}\)
Xác suất để lấy ra được viên bi màu đỏ có đánh số là \(P\left( A\mid B \right)\)
Xác suất để viên bi được lấy ra có đánh số là \(P\left( A \right)=\frac{7}{16}\)
Câu 16:
Hệ thống phòng không "Vòm sắt" là một trong những hệ thống đánh chặn tên lửa từ xa rất nổi tiếng của Israel. Để "Vòm sắt" hoạt động được chính xác người ta trang bị một Radar có khả năng phát hiện tên lửa với bán kính 417 km. Trong hệ trục tọa độ \(Oxyz\) một hệ thống "Vòm sắt" đang ở vị trí \(O\left( 0;0;0 \right)\) và một quả tên lửa đang ở vị trí \(A\left( 688;185;-8 \right)\) được phóng lên và bay theo một quỹ đạo là đường thẳng có vectơ chỉ phương là \(\vec{u}=\left( -91;-75;0 \right)\).
Trong các mệnh đề sau, mệnh đề nào đúng, mệnh đề nào sai?
Phương trình mặt cầu thể hiện vùng phủ sóng của Radar là \({{x}^{2}}+{{y}^{2}}+{{z}^{2}}=417\)
Radar phát hiện một quả tên lửa ngay tại vị trí được phóng lên
Giả sử hệ thống "Vòm sắt" gặp trục trặc không thể bắn hạ quả tên lửa khi đó vị trí cuối cùng quả tên lửa xuất hiện trên màn hình radar là \(B\left( 415;-40;-8 \right)\)
Nếu hệ thống gặp trục trặc không bắn hạ được tên lửa thì khoảng cách gần nhất từ hệ thống "Vòm sắt" đến quả tên lửa là \(\approx 190\text{km}\)