Đề thi thử Tốt nghiệp THPT năm 2025 môn Toán Sở GD&ĐT TP. Cần Thơ - Đề 3
22 câu hỏi 60 phút
Nguyên hàm của hàm số \(f\left( x \right)={{e}^{x}}\) là:
\(\frac{{{e}^{x+1}}}{x+1}+C\)
\({{e}^{x}}+C\)
\(\frac{{{e}^{x}}}{x}+C\)
\(x\cdot {{e}^{x-1}}+C\)
Nguyên hàm của \({{e}^{x}}\) là \({{e}^{x}}+C\).
Danh sách câu hỏi:
Nguyên hàm của \({{e}^{x}}\) là \({{e}^{x}}+C\).
Thể tích khối tròn xoay được tạo thành khi quay hình phẳng \(\left( H \right)\) giới hạn bởi đồ thị hàm số \(y=f\left( x \right)\), trục hoành và hai đường thẳng \(x=a\), \(x=b\) quanh trục Ox được tính theo công thức: \(V=\pi \underset{a}{\overset{b}{\mathop{\int }}}\,{{\left[ f\left( x \right) \right]}^{2}}dx\).
Mẫu số liệu \({{M}_{1}}\) có \({{n}_{{{M}_{1}}}}=3+4+8+6+4=25\).
Số trung bình của mẫu số liệu \({{M}_{1}}\) là:
\(\overline{{{x}_{{{M}_{1}}}}}=\frac{3.9+4.11+8.13+6.15+4.17}{25}=13,32\).
Phương sai của mẫu số liệu \({{M}_{1}}\) là:
\(s_2^2=\frac{6(9-13,32)^2+8(11-13,32)^2+16(13-13,32)^2+12(15-13,32)^2+8(17-13,32)^2}{50}=5,9776\)
Suy ra độ lệch chuẩn của mẫu số liệu \({{M}_{1}}\) là:
\({{s}_{1}}=\sqrt{{{s}_{1}}^{2}}=\sqrt{5,9776}\approx 2,44\).
Mẫu số liệu \({{M}_{2}}\) có \({{n}_{{{M}_{2}}}}=6+8+16+12+8=50\).
Số trung bình của mẫu số liệu \({{M}_{2}}\) là:
\(\overline{{{x}_{{{M}_{2}}}}}=\frac{6.9+8.11+16.13+12.15+8.17}{50}=13,32.\)
Phương sai của mẫu số liệu \({{M}_{2}}\) là:
\(s_2^2=\frac{6(9-13,32)^2+8(11-13,32)^2+16(13-13,32)^2+12(15-13,32)^2+8(17-13,32)^2}{50}=5,9776\)
Suy ra độ lệch chuẩn của mẫu số liệu \({{M}_{2}}\) là:
\({{s}_{2}}=\sqrt{{{s}_{2}}^{2}}=\sqrt{5,9776}\approx 2,44\).
Vậy \({{s}_{1}}={{s}_{2}}\).
Phương trình đường thẳng đi qua điểm \(M\left( 1;-3;5 \right)\) và có một vectơ chỉ phương \(\left( 2;-1;1 \right)\) là:
\(\frac{x-1}{2}=\frac{y+3}{-1}=\frac{z-5}{1}\).
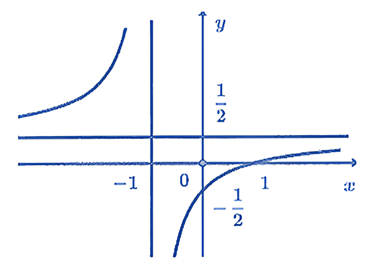
Tiệm cận ngang của đồ thị hàm số là: \(y=\frac{1}{2}\).
Câu 11:
Cho hình hộp \(ABCD\cdot {A}'{B}'{C}'{D}'\) (minh họa như hình sau). Phát biểu nào sau đây là sai?

Câu 13:
Cho hàm số \(f\left( x \right)=2\text{cos}x+x\)
\(f\left( 0 \right)=2;f\left( \frac{\pi }{2} \right)=\frac{\pi }{2}\)
Đạo hàm của hàm số đã cho là \({f}'\left( x \right)-2\text{sin}x+1\)
Nghiệm của phương trình \({f}'\left( x \right)=0\) trên đoạn \(\left[ 0;\frac{\pi }{2} \right]\) là \(\frac{\pi }{6}\)
Giá trị lớn nhất của \(f\left( x \right)\) trên đoạn \(\left[ 0;\frac{\pi }{2} \right]\) là \(\sqrt{3}+\frac{\pi }{6}\)
Câu 14:
Một người điều khiển ô tô đang ở đường dẫn muốn nhập làn vào đường cao tốc. Khi ô tô cách điểm nhập làn 200 m, tốc độ của ô tô là \(36\text{ }\!\!~\!\!\text{ km}/\text{h}\). Hai giây sau đó, ô tô bắt đầu tăng tốc với tốc độ \(v\left( t \right)=at+b\) \((a,b\in \mathbb{R},a>0)\), trong đó \(t\) là thời gian tính bằng giây kể từ khi bắt đầu tăng tốc. Biết rằng ô tô nhập làn cao tốc sau 12 giây và duy trì sự tăng tốc trong 24 giây kể từ khi bắt đầu tăng tốc
Quãng đường ô tô đi được từ khi bắt đầu tăng tốc đến khi nhập làn là 180 m
Giá trị của \(b\) là 10
Quãng đường \(S\left( t \right)\) (đơn vị: mét) mà ô tô đi được trong thời gian \(t\) giây \(\left( 0\le t\le 24 \right)\) kể từ khi tăng tốc được tính theo công thức \(S\left( t \right)=\int_{0}^{24}{v}\left( t \right)dt\)
Sau 24 giây kể từ khi tăng tốc, tốc độ của ô tô không vượt quá tốc độ tối đa cho phép là \(100\text{ }\!\!~\!\!\text{ km}/\text{h}\)
Câu 15:
Trước khi đưa một loại sản phẩm ra thị trường, người ta đã phỏng vấn ngẫu nhiên 200 khách hàng về sản phầm đó. Kết quả thống kê như sau: có 105 người trả lời "sẽ mua"; có 95 người trả lời "không mua". Kinh nghiệm cho thấy tỉ lệ khách hàng thực sự sẽ mua sản phẩm tương ứng với những cách trả lời "sẽ mua" và "không mua" lần lượt là \(70\%\) và \(30\%\).
Gọi \(A\) là biến cố "Người được phỏng vấn thực sự sẽ mua sản phẩm".
Gọi \(B\) là biến cố "Người được phỏng vấn trả lời sẽ mua sản phẩm"
Xác suất \(P\left( B \right)=\frac{21}{40}\) và \(P\left( \overline{B} \right)=\frac{19}{40}\)
Xác suất có điều kiện \(P\left( A\mid B \right)=0,3\)
Xác suất \(P\left( A \right)=0,51\)
Trong số những người được phỏng vấn thực sự sẽ mua sản phẩm có \(70\%\) người đã trả lời "sẽ mua" khi được phỏng vấn (kết quả tính theo phần trăm được làm tròn đến hàng đơn vị)
Câu 16:
Các thiên thạch có đường kính lớn hơn \(140~m\) và có thể lại gần Trái Đất ở khoảng cách nhỏ hơn \(7 ~500~ 000~ km\) được coi là những vật thể có khả năng va chạm gây nguy hiểm cho Trái Đất. Để theo dõi những thiên thạch này, người ta đã thiết lập các trạm quan sát các vật thể bay gần Trái Đất. Giả sử có một hệ thống quan sát có khả năng theo dõi các vật thể ở độ cao không vượt quá \(6 ~600 ~km\) so với mực nước biển. Coi Trái Đất là khối cầu có bán kính \(6 ~400 ~km\). Chọn hệ trục tọa độ \(Oxyz\) trong không gian có gốc \(O\) tại tâm Trái Đất và đơn vị độ dài trên mỗi trục tọa độ là \(1000 ~km\). Một thiên thạch (coi như một hạt) chuyển động với tốc độ không đổi theo một đường thẳng từ điểm \(M\left( 6;20;0 \right)\) đến điểm \(N\left( -6;-12;16 \right)\).
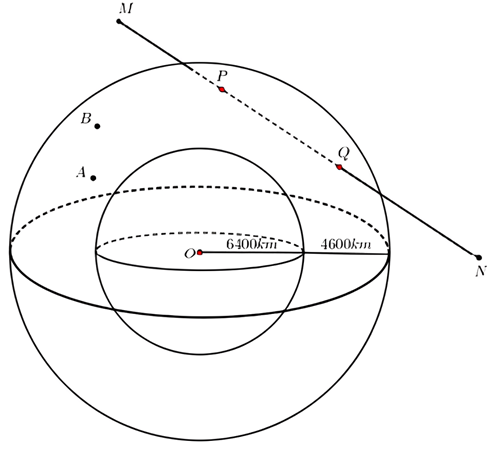
Đường thẳng \(MN\) có phương trình tham số là \(\left\{ \begin{array}{*{35}{l}} x=6+3t \\ y=20+8t,\left( t\in \mathbb{R} \right) \\ z=-4t \\\end{array} \right.\)
Vị trí đầu tiên thiên thạch di chuyển vào phạm vi theo dõi của hệ thống quan sát là điểm \(A\left( -3;-4;12 \right)\)
Khoảng cách giữa vị trí đầu tiên và vị trí cuối cùng mà thiên thạch di chuyển trong phạm vi theo dõi của hệ thống quan sát là 18 900 km (kết quả làm tròn đến hàng trăm theo đơn vị ki-lô-mét)
Nếu thời gian di chuyển của thiên thạch trong phạm vi theo dõi của hệ thống quan sát là 3 phút thì thời gian nó di chuyển từ \(M\) đến \(N\) là 6 phút