Đề thi thử Tốt nghiệp THPT năm 2025 môn Toán Sở GD&ĐT TP. Cần Thơ - Đề 2
22 câu hỏi 60 phút
Phương trình \({{2}^{2{{x}^{2}}+5x+4}}=4\) có tổng tất cả các nghiệm bằng:
\(-1\)
\(\frac{5}{2}\)
\(-\frac{5}{2}\)
\(1\)
Ta có:
\({{2}^{2{{x}^{2}}+5x+4}}=4 \\ \Leftrightarrow 2{{x}^{2}}+5x+4=2 \\ \Leftrightarrow 2{{x}^{2}}+5x+2=0 \\ \Leftrightarrow \left[ \begin{align} & x=-2 \\ & x=-\frac{1}{2} \\ \end{align} \right.\)
Vậy tổng tất cả các nghiệm bằng \(-\frac{5}{2}\).
Danh sách câu hỏi:
Ta có:
\({{2}^{2{{x}^{2}}+5x+4}}=4 \\ \Leftrightarrow 2{{x}^{2}}+5x+4=2 \\ \Leftrightarrow 2{{x}^{2}}+5x+2=0 \\ \Leftrightarrow \left[ \begin{align} & x=-2 \\ & x=-\frac{1}{2} \\ \end{align} \right.\)
Vậy tổng tất cả các nghiệm bằng \(-\frac{5}{2}\).
Ta có \(\int{\left( x-\frac{1}{x} \right)\text{d}x}=\frac{1}{2}{{x}^{2}}-\ln \left| x \right|+C\).
Tứ phân vị thứ nhất của mẫu số liệu gốc là \(\frac{{{x}_{5}}+{{x}_{6}}}{2}\).
Do \({{x}_{5}},{{x}_{6}}\) đều thuộc nhóm \(\left[ 16;17 \right)\) nên nhóm chứa tứ phân vị thứ nhất là nhóm \(\left[ 16;17 \right)\).
Ta có: \({{u}_{4}}={{u}_{1}}+3d=2+3.5=17\).
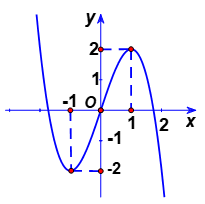
Dựa vào đồ thị suy ra hàm số tăng trên khoảng \(\left( -1;1 \right)\).
Câu 13:
Cho hàm số \(f\left( x \right)=2\text{cos}x+x\). Xét tính đúng sai của các phát biểu sau:
\(f\left( 0 \right)=2;f\left( \frac{\pi }{2} \right)=\frac{\pi }{2}\)
Đạo hàm của hàm số đã cho là \({f}'\left( x \right)=2\text{sin}x+1\)
Nghiệm của phương trình \({f}'\left( x \right)=0\) trên đoạn \(\left[ 0;\frac{\pi }{2} \right]\) là \(\frac{5\pi }{6}\)
Giá trị lớn nhất của \(f\left( x \right)\) trên đoạn \(\left[ 0;\frac{\pi }{2} \right]\) là \(\sqrt{3}+\frac{5\pi }{6}\)
Câu 14:
Một người điều khiển ô tô đang ở đường dẫn muốn nhập làn vào đường cao tốc. Khi ô tô cách điểm nhập làn 215 m, tốc độ của ô tô là 54 km/h. 1 giây sau đó, ô tô bắt đầu tăng tốc với tốc độ \(v\left( t \right)=at+b\) (\(a,b\in \mathbb{R},a>0\)), trong đó \(t\) là thời gian tính bằng giây kể từ khi bắt đầu tăng tốc. Biết rằng ô tô nhập làn cao tốc sau 13 giây và duy trì sự tăng tốc trong 17 giây kể từ khi bắt đầu tăng tốc. Xét tính đúng sai của các phát biểu sau:
Quãng đường ô tô đi được từ khi bắt đầu tăng tốc đến khi nhập làn là 190 m
Giá trị của \(b\) là 15
Quãng đường \(S\left( t \right)\) (đơn vị: mét) mà ô tô đi được trong thời gian \(t\) giây (\(0\le t\le 17\)) kể từ khi tăng tốc được tính theo công thức \(S\left( t \right)=\mathop{\int }_{0}^{17}v\left( x \right)dx\)
Sau 17 giây kể từ khi tăng tốc, tốc độ của ô tô vượt quá tốc độ tối đa cho phép là 100 km/h
Câu 15:
Một công ty tham gia đấu thầu 2 dự án với xác suất thắng thầu của dự án 1 là \(0,4\) và của dự án 2 là \(0,6\) . Xác suất để công ty thắng cả 2 dự án là \(0,24\).
Gọi \(A\) là biến cố: "Thắng thầu dự án 1".
Gọi \(B\) là biến cố: "Thắng thầu dự án 2"
Các biến cố \(A\) và \(B\) là độc lập
Xác suất để công ty thắng thầu đúng 1 dự án là 0,52
Xác suất để công ty thắng thầu dự án 2 biết công ty thắng thầu dự án 1 là 0,6
Xác suất để công ty thắng thầu dự án 2 biết công ty không thắng thầu dự án 1 là 0,4
Câu 16:
Trong không gian với hệ tọa độ \(Oxyz\), một cabin cáp treo xuất phát từ điểm \(A\left( 1,2,3 \right)\) và chuyển động đều theo đường cáp có véc tơ chỉ phương \(\vec{u}=\left( 3,-4,2 \right)\) với tốc độ \(5\text{ }\!\!~\!\!\text{ m}/\text{s}\)
Phương trình tham số của đường cáp là: \(\left\{ \begin{align} & x=1+3t \\ & y=2-4t \\ & z=3+2t \\ \end{align} \right.\)
Sau thời gian \(t=100\) giây kể từ khi xuất phát, tọa độ điểm M mà cabin đến được là \(M\left( 301,-398,203 \right)\)
Cabin dừng ở điểm \(B\) có hoành độ 301, quãng đường từ \(A\) đến \(B\) dài 500 m
Đường cáp \(AB\) tạo với mặt phẳng \((Oxyz)\) một góc \({{30}^{o}}\)