Câu hỏi:
Cho khối chóp \(O.ABC\) có \(OA\) vuông góc với mặt phẳng \(\left( ABC \right)\), tam giác \(ABC\) vuông tại \(A\) và \(OA=2,AB=3,AC=6\). Thể tích của khối chóp \(O.ABC\) bằng
Đáp án đúng: B
Thể tích khối chóp được tính bằng công thức: \(V=\frac{1}{3}\cdot \text {Diện tích đáy} \cdot \text{Chiều cao}\).
Diện tích đáy (tam giác vuông ABC) là: \(S=\frac{1}{2}.3.6=9\).
Chiều cao \(\text{OA}=2\).
Vậy thể tích khối chóp là: \(V=\frac{1}{3}.9.2=6\).
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Đề Thi Tốt Nghiệp THPT Quốc Gia Năm 2025 - Toán có cấu trúc bám sát theo ma trận kiến thức của Bộ GD-ĐT. Ngoài ra, đề cũng xuất hiện nhiều bài toán thực tế có gắn liền với cuộc sống. Trong đề có 12 câu trắc nghiệm nhiều phương án trả lời bao quát kiến thức lớp 11, 12; 4 câu trắc nghiệm Đúng – Sai cũng thuộc chương trình 12 và 6 câu trắc nghiệm trả lời ngắn bao quát kiến thức lớp 10, 11 và 12. Các chuyên đề trọng điểm như hàm số, đạo hàm, tích phân, phương trình bậc hai, hình học không gian, tổ hợp - xác suất, số phức và phương pháp tọa độ được đưa vào đầy đủ trong đề thi.
Câu hỏi liên quan
Một phần mềm nhận dạng tin nhắn quảng cáo trên điện thoại bằng cách dựa theo từ khóa để đánh dấu một số tin nhắn được gửi đến. Qua một thời gian dài sử dụng, người ta thấy rằng trong số tất cả các tin nhắn gửi đến, có \(20\%\) số tin nhắn bị đánh dấu. Trong số các tin nhắn bị đánh dấu, có \(10\%\) số tin nhắn không phải là quảng cáo. Trong số các tin nhắn không bị đánh dấu, có \(10\%\) số tin nhắn là quảng cáo.
Chọn ngẫu nhiên một tin nhắn được gửi đến điện thoại.
Xác suất để tin nhắn đó không bị đánh dấu bằng \(0,8\)
Xác suất để tin nhắn đó không phải là quảng cáo, biết rằng nó không bị đánh dấu, bằng \(0,95\)
Xác suất để tin nhắn đó không phải là quảng cáo bằng \(0,76\)
Xác suất để tin nhắn đó không bị đánh đấu, biết rằng nó không phải là quảng cáo, nhỏ hơn \(0,95\)
1. Xác định các sự kiện: Gọi A là tin nhắn bị đánh dấu, \(\bar{A}\) là tin nhắn không bị đánh dấu, B là tin nhắn quảng cáo, \(\bar{B}\) là tin nhắn không phải quảng cáo.
2. Xác suất đã cho:
\(P(A)=0.2,P(\bar{A})=0.8,P(\bar{B}|A)=0.1,P(B|\bar{A})=0.1\).
3. Kiểm tra từng phát biểu:
- a) \(P(\bar{A})=0,8\) (Đúng)
- b) Tính \(P(\bar{B}|\bar{A})=1-P(B|\bar{A})=0,9\) (Sai)
- c) Tính \(P(\bar{B})=P(\bar{B}|A)P(A)+P(\bar{B}|\bar{A})P(\bar{A})=0,74\) (Sai)
- d) Tính \(P(\bar{A}|\bar{B})=\frac{P(\bar{B}|\bar{A})P(\bar{A})}{P(\bar{B})}\approx 0,973\) (Sai)
Cho hàm số \(f\left( x \right)={{x}^{3}}-27x+81\).
Hàm số đã cho có đạo hàm là \({f}'\left( x \right)=3{{x}^{2}}-27\)
Phương trình \({f}'\left( x \right)=0\) có tập nghiệm là \(S=\left\{ 3 \right\}\)
\(f\left( 3 \right)=27\)
Giá trị nhỏ nhất của hàm số \(f\left( x \right)\) trên đoạn \(\left[ -4;4 \right]\) bằng 27
a) Đúng. Tính đạo hàm của hàm số \(f(x)={{x}^{3}}-27x+81\).
Ta có: \({f}'(x)=3{{x}^{2}}-27\).
b) Sai. Giải phương trình \(3{{x}^{2}}-27=0\), ta được: \({{x}^{2}}=9=>x=\pm 3\).
Vậy tập nghiệm của phương trình \({f}'(x)=0\) là \(S=-3;3\).
c) Đúng. Tính giá trị của hàm số tại \(x = 3\):
\(f(3)={{(3)}^{3}}-27(3)+81=27-81+81=27\).
d) Đúng. Tính giá trị của hàm số tại các điểm tới hạn và hai đầu mút của đoạn [-4; 4]:
\(f(-4)={{(-4)}^{3}}-27(-4)+81=-64+108+81=125\)
\(f(3)=27\)
\(f(-3)={{(-3)}^{3}}-27(-3)+81=-27+81+81=135\)
\(f(4)={{(4)}^{3}}-27(4)+81=64-108+81=37\)
So sánh các giá trị này, ta thấy giá trị nhỏ nhất của \(f(x)\) trên đoạn \([-4;4]\) là \(27\).
Đối với ngành nuôi trồng thủy sản, việc kiểm soát lượng thuốc tồn dư trong nước là một nhiệm vụ quan trọng nhằm đáp ứng các tiêu chuẩn an toàn về môi trường. Khi nghiên cứu một loại thuốc trị bệnh trong nuôi trồng thủy sản, người ta sử dụng thuốc đó một lần và theo dõi nồng độ thuốc tồn dư trong nước kể từ lúc sử dụng thuốc. Kết quả cho thấy nồng độ thuốc \(y\left( t \right)\) (đơn vị: mg/lit) tồn dư trong nước tại thời điểm \(t\) ngày \(\left( t\ge 0 \right)\) kể từ lúc sử dụng thuốc, thỏa mãn \(y\left( t \right)>0\) và \({y}'\left( t \right)=k.y\left( t \right)\) \(\left( t\ge 0 \right)\), trong đó \(k\) là hằng số khác không. Đo nồng độ thuốc tồn dư trong nước tại các thời điểm \(t=6\) (ngày); \(t=12\) (ngày) nhận được kết quả lần lượt là 2mg/lit; 1mg/lit. Cho biết \(y\left( t \right)={{e}^{g\left( t \right)}}\left( t\ge 0 \right)\).
\(g\left( t \right)=kt+C\left( t\ge 0 \right)\) với \(C\) là một hằng số xác định
\(k=-\frac{\ln 2}{6}\)
\(C=3\ln 2\)
Nồng độ thuốc tồn dư trong nước tại thời điểm \(t=20\) (ngày) kể từ lúc sử dụng thuốc lớn hơn \(0,4\) mg/lit
a) Ta có \(y(t)={{e}^{g(t)}}\Rightarrow {{y}^{\prime }}(t)={{g}^{\prime }}(t)\cdot {{e}^{g(t)}}\).
Thay vào \({{y}^{\prime }}(t)=k\cdot y(t)\Rightarrow {{g}^{\prime }}(t)\cdot {{e}^{g(t)}}=k\cdot {{e}^{g(t)}}\Leftrightarrow {{g}^{\prime }}(t)=k\)
\(\Rightarrow g(t)=\int{{{g}^{\prime }}}(t)dt=\int{k}dt=kt+C\) với \(C\) là một hằng số xác định.
b) và c) Ta có \(y(t)={{e}^{g(t)}}\Leftrightarrow g(t)=\ln y(t)\)
\(\Rightarrow \left\{ \begin{array}{*{35}{l}} y(6)=2 \\ y(12)=1 \\\end{array}\Leftrightarrow \left\{ \begin{array}{*{35}{l}} g(6)=\ln 2 \\ g(12)=0 \\\end{array} \right. \right.\) \(\Leftrightarrow \left\{ \begin{array}{*{35}{l}} 6k+C=\ln 2 \\ 12k+C=0 \\\end{array}\Leftrightarrow \left\{ \begin{array}{*{35}{l}} k=-\frac{\ln 2}{6} \\ C=2\ln 2 \\\end{array} \right. \right.\).
d) Ta có \(g(t)=-\frac{\ln 2}{6}t+2\ln 2\)
\(\Rightarrow y(t)={{e}^{-\frac{\ln 2}{6}t+2\ln 2}}\Rightarrow y(20)\approx 0,39\) mg/lít \(<0,4\) mg/lít.
Mô hình toán học sau đây được sử dụng trong quan sát chuyển động của một vật. Trong không gian cho hệ tọa độ \(Oxyz\) có \(\vec{i},\vec{j},\vec{k}\) lần lượt là các vectơ đơn vị trên các trục \(Ox,Oy,Oz\) và độ dài của mỗi vectơ đơn vị đó bằng 1 mét. Cho hai điểm \(A\) và \(B\), trong đó điểm \(A\) có tọa độ là \(\left( 6;6;0 \right)\). Một vật (coi như là một hạt) chuyển động thẳng với tốc độ phụ thuộc thời gian \(t\) (giây) theo công thức \(v\left( t \right)=\beta t+300\) (m/giây), trong đó \(\beta \) là hằng số dương và \(0\le t\le 6\). Ở thời điểm ban đầu \(\left( t=0 \right)\), vật đi qua \(A\) với tốc độ \(300\) m/giây và hướng tới \(B\). Sau \(2\) giây kể từ thời điểm ban đầu, vật đi được quãng đường \(608~m\). Gọi \(\vec{u}=\left( a;b;c \right)\) là vectơ cùng hướng với vectơ \(\overrightarrow{AB}\). Biết rằng \(\left| {\vec{u}} \right|=1\) và góc giữa vectơ \(\vec{u}\) lần lượt với các vectơ \(\vec{i},\vec{j},\vec{k}\) có số đo tương ứng bằng \({{60}^{\circ }},{{60}^{\circ }},{{45}^{\circ }}\).
\(a=\cos {{60}^{\circ }}\)
Phương trình đường thẳng \(AB\) là \(\frac{x-6}{1}=\frac{y-6}{1}=\frac{z}{2}\)
\(\beta =3\)
Giả sử sau 5 giây kể từ thời điểm ban đầu, vật đến điểm \(B\left( {{x}_{B}};{{y}_{B}};{{z}_{B}} \right)\). Khi đó \({{x}_{B}}=781\)
a) Với \(\vec{u}=\overrightarrow{OE}=(a;b;c)\) và \(|\vec{u}|=OE=1\) và góc giữa vectơ \(\vec{u}\) lần lượt với các vectơ \(\vec{i},\vec{j},\vec{k}\) có số đo tương ứng bằng \({{60}^{{}^\circ }},{{60}^{{}^\circ }},{{45}^{{}^\circ }}\Rightarrow \widehat{AOE}={{60}^{{}^\circ }},\widehat{COE}={{60}^{{}^\circ }},\widehat{GOE}={{45}^{{}^\circ }}\)
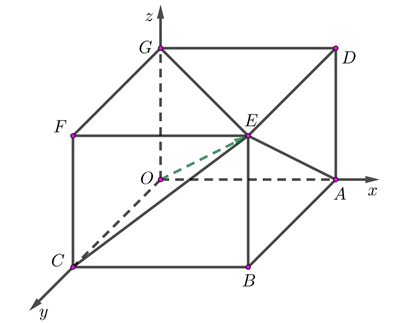
b) Ta có \(\overrightarrow{AB}//\vec{u}\left( \frac{1}{2};\frac{1}{2};\frac{\sqrt{2}}{2} \right)=(1;1;\sqrt{2})\Rightarrow AB:\frac{x-6}{1}=\frac{y-6}{1}=\frac{z}{\sqrt{2}}\).
c) Quãng đường đi được trong 2 giây là
\(s=\int_{0}^{2}{|v(t)|dt}=\int_{0}^{2}{(\beta t+300)dt}=608\Leftrightarrow \beta =4\)
d) Quãng đường đi được trong 5 giây là
\(AB=\int_{0}^{5}{|v(t)|dt}=\int_{0}^{5}{(4t+300)dt}=1550~\text{m}\)
\(\Rightarrow \overrightarrow{AB}=\frac{AB}{|\vec{u}|}\cdot \vec{u}=\frac{1550}{1}\cdot \left( \frac{1}{2};\frac{1}{2};\frac{\sqrt{2}}{2} \right)\Rightarrow {{x}_{B}}=\frac{1550}{2}+6=781\)
Chọn hệ tọa độ Oxyz sao cho gốc O trùng với điểm A, trục Ox trùng với cạnh AB, trục Oy trùng với cạnh AD, và trục Oz vuông góc với mặt phẳng (ABCD). Khi đó, ta có tọa độ các điểm như sau: A(0,0,0), B(2,0,0), C(2,2,0), D(0,2,0).
Vì H là trọng tâm tam giác ABC nên tọa độ của H là \((\frac{0+2+2}{3},\frac{0+0+2}{3},0)=(\frac{4}{3},\frac{2}{3},0).\)
Vì SH vuông góc với (ABCD) và \(SH = \sqrt{2}\) nên tọa độ của S là \((\frac{4}{3},\frac{2}{3},\sqrt{2})\)
Vectơ chỉ phương của AC là \(\overrightarrow{AC}=C-A=(2,2,0).\)
Vectơ chỉ phương của SD là:
\(\overrightarrow{SD}=D-S=(0-\frac{4}{3},2-\frac{2}{3},0-\sqrt{2})=(-\frac{4}{3},\frac{4}{3},-\sqrt{2}).\)
Tích có hướng của \(\overrightarrow{AC}\) và \(\overrightarrow{SD}\) là
\(\begin{array}{*{35}{l}} \vec{n}=\overrightarrow{AC}\times \overrightarrow{SD} & =(2,2,0)\times (-\frac{4}{3},\frac{4}{3},-\sqrt{2}) \\ {} & =(-2\sqrt{2},2\sqrt{2},\frac{8}{3}-(-\frac{8}{3})) \\ {} & =(-2\sqrt{2},2\sqrt{2},\frac{16}{3}). \\\end{array}\)
Chọn điểm \(A(0,0,0)\) trên AC và điểm \(S(\frac{4}{3},\frac{2}{3},\sqrt{2})\) trên SD.
\(\overrightarrow{AS}=S-A=(\frac{4}{3},\frac{2}{3},\sqrt{2}).\)
Khoảng cách giữa hai đường thẳng AC và SD là
\(\begin{array}{*{35}{l}} d(AC,SD) & =\frac{|\overrightarrow{AS}.[\overrightarrow{AC},\overrightarrow{SD}]|}{|[\overrightarrow{AC},\overrightarrow{SD}]|} \\ {} & =\frac{\left| \left( \frac{4}{3},\frac{2}{3},\sqrt{2} \right)\cdot -\left( 2\sqrt{2},2\sqrt{2},\frac{16}{3} \right) \right|}{\sqrt{8+8+\frac{256}{9}}} \\ {} & =\frac{\left| \frac{-8\sqrt{2}}{3}+\frac{4\sqrt{2}}{3}+\frac{16\sqrt{2}}{3} \right|}{\sqrt{\frac{144+256}{9}}}\text{ }=\frac{4\sqrt{2}}{\sqrt{\frac{400}{9}}}\approx 0,85. \\\end{array}\)
Vậy khoảng cách giữa hai đường thẳng AC và SD là \(0,85\).
Bộ 50 Đề Thi Thử Tốt Nghiệp THPT Giáo Dục Kinh Tế Và Pháp Luật Năm 2026 – Theo Cấu Trúc Đề Minh Họa Bộ GD&ĐT
Bộ 50 Đề Thi Thử Tốt Nghiệp THPT Lịch Sử Học Năm 2026 – Theo Cấu Trúc Đề Minh Họa Bộ GD&ĐT
Bộ 50 Đề Thi Thử Tốt Nghiệp THPT Công Nghệ Năm 2026 – Theo Cấu Trúc Đề Minh Họa Bộ GD&ĐT
Bộ 50 Đề Thi Thử Tốt Nghiệp THPT Môn Hóa Học Năm 2026 – Theo Cấu Trúc Đề Minh Họa Bộ GD&ĐT
Bộ 50 Đề Thi Thử Tốt Nghiệp THPT Môn Sinh Học Năm 2026 – Theo Cấu Trúc Đề Minh Họa Bộ GD&ĐT
