Câu hỏi:
Mô hình toán học sau đây được sử dụng trong quan sát chuyển động của một vật. Trong không gian cho hệ tọa độ \(Oxyz\) có \(\vec{i},\vec{j},\vec{k}\) lần lượt là các vectơ đơn vị trên các trục \(Ox,Oy,Oz\) và độ dài của mỗi vectơ đơn vị đó bằng 1 mét. Cho hai điểm \(A\) và \(B\), trong đó điểm \(A\) có tọa độ là \(\left( 6;6;0 \right)\). Một vật (coi như là một hạt) chuyển động thẳng với tốc độ phụ thuộc thời gian \(t\) (giây) theo công thức \(v\left( t \right)=\beta t+300\) (m/giây), trong đó \(\beta \) là hằng số dương và \(0\le t\le 6\). Ở thời điểm ban đầu \(\left( t=0 \right)\), vật đi qua \(A\) với tốc độ \(300\) m/giây và hướng tới \(B\). Sau \(2\) giây kể từ thời điểm ban đầu, vật đi được quãng đường \(608~m\). Gọi \(\vec{u}=\left( a;b;c \right)\) là vectơ cùng hướng với vectơ \(\overrightarrow{AB}\). Biết rằng \(\left| {\vec{u}} \right|=1\) và góc giữa vectơ \(\vec{u}\) lần lượt với các vectơ \(\vec{i},\vec{j},\vec{k}\) có số đo tương ứng bằng \({{60}^{\circ }},{{60}^{\circ }},{{45}^{\circ }}\).
Đáp án đúng: Đúng, Sai, Sai, Đúng
a) Với \(\vec{u}=\overrightarrow{OE}=(a;b;c)\) và \(|\vec{u}|=OE=1\) và góc giữa vectơ \(\vec{u}\) lần lượt với các vectơ \(\vec{i},\vec{j},\vec{k}\) có số đo tương ứng bằng \({{60}^{{}^\circ }},{{60}^{{}^\circ }},{{45}^{{}^\circ }}\Rightarrow \widehat{AOE}={{60}^{{}^\circ }},\widehat{COE}={{60}^{{}^\circ }},\widehat{GOE}={{45}^{{}^\circ }}\)
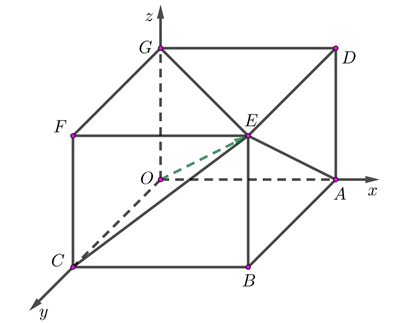
b) Ta có \(\overrightarrow{AB}//\vec{u}\left( \frac{1}{2};\frac{1}{2};\frac{\sqrt{2}}{2} \right)=(1;1;\sqrt{2})\Rightarrow AB:\frac{x-6}{1}=\frac{y-6}{1}=\frac{z}{\sqrt{2}}\).
c) Quãng đường đi được trong 2 giây là
\(s=\int_{0}^{2}{|v(t)|dt}=\int_{0}^{2}{(\beta t+300)dt}=608\Leftrightarrow \beta =4\)
d) Quãng đường đi được trong 5 giây là
\(AB=\int_{0}^{5}{|v(t)|dt}=\int_{0}^{5}{(4t+300)dt}=1550~\text{m}\)
\(\Rightarrow \overrightarrow{AB}=\frac{AB}{|\vec{u}|}\cdot \vec{u}=\frac{1550}{1}\cdot \left( \frac{1}{2};\frac{1}{2};\frac{\sqrt{2}}{2} \right)\Rightarrow {{x}_{B}}=\frac{1550}{2}+6=781\)
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Đề Thi Tốt Nghiệp THPT Quốc Gia Năm 2025 - Toán có cấu trúc bám sát theo ma trận kiến thức của Bộ GD-ĐT. Ngoài ra, đề cũng xuất hiện nhiều bài toán thực tế có gắn liền với cuộc sống. Trong đề có 12 câu trắc nghiệm nhiều phương án trả lời bao quát kiến thức lớp 11, 12; 4 câu trắc nghiệm Đúng – Sai cũng thuộc chương trình 12 và 6 câu trắc nghiệm trả lời ngắn bao quát kiến thức lớp 10, 11 và 12. Các chuyên đề trọng điểm như hàm số, đạo hàm, tích phân, phương trình bậc hai, hình học không gian, tổ hợp - xác suất, số phức và phương pháp tọa độ được đưa vào đầy đủ trong đề thi.
Câu hỏi liên quan

Bộ 50 Đề Thi Thử Tốt Nghiệp THPT Giáo Dục Kinh Tế Và Pháp Luật Năm 2026 – Theo Cấu Trúc Đề Minh Họa Bộ GD&ĐT

Bộ 50 Đề Thi Thử Tốt Nghiệp THPT Lịch Sử Học Năm 2026 – Theo Cấu Trúc Đề Minh Họa Bộ GD&ĐT

Bộ 50 Đề Thi Thử Tốt Nghiệp THPT Công Nghệ Năm 2026 – Theo Cấu Trúc Đề Minh Họa Bộ GD&ĐT

Bộ 50 Đề Thi Thử Tốt Nghiệp THPT Môn Hóa Học Năm 2026 – Theo Cấu Trúc Đề Minh Họa Bộ GD&ĐT

Bộ 50 Đề Thi Thử Tốt Nghiệp THPT Môn Sinh Học Năm 2026 – Theo Cấu Trúc Đề Minh Họa Bộ GD&ĐT