Câu hỏi:
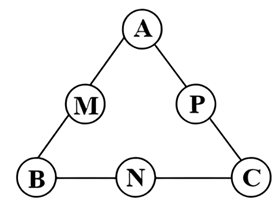
Bạn Nam tham gia cuộc thi giải một mật thư. Theo quy tắc của cuộc thi, người chơi cần chọn ra sáu số từ tập \(S=\left\{ 21;22;23;24;25;26;27;28;29 \right\}\) và xếp mỗi số vào đúng một vị trí trong sáu vị trí \(A,B,C,M,N,P\) như hình bên sao cho mỗi vị trí chỉ được xếp một số. Mật thư sẽ được giải nếu các bộ ba số xuất hiện ở những bộ ba vị trí \(\left( A,M,B \right);\left( B,N,C \right);\left( C,P,A \right)\) tạo thành các cấp số cộng theo thứ tự đó. Bạn Nam chọn ngẫu nhiên sáu số trong tập \(S\) và xếp ngẫu nhiên vào các vị trí được yêu cầu. Gọi xác suất để bạn Nam giải được mật thư ở lần chọn và xếp đó là \(a\). Giá trị của \(\frac{2}{a}\) bằng bao nhiêu?
Đáp án đúng: 2520
Số phần tử của không gian mẫu: \(n\left( \text{ }\!\!\Omega\!\!\text{ } \right)=A_{9}^{6}=60480\) (cách)
Để giải được mật thư, các số được chọn và xếp phải thỏa mãn cấp số cộng \(\left\{ \begin{array}{*{35}{l}} A+B=2M \\ B+C=2N \\ C+A=2P \\\end{array} \right.\)
Do đó tổng \(A+B;B+C;C+A\) phải là các số chẵn (Điều này xảy ra khi \(A,B,C\) phải cùng chẵn hoặc cùng lẻ)
Suy ra ta phải đi tìm bộ 6 số phân biệt \(\left\{ A,B,C,M,N,P \right\}\) trong \(S\) thỏa mãn điều kiện:
Trong tập \(S\) có \(\left\{ \begin{array}{*{35}{l}} L=\left\{ 21;23;25;27;29 \right\} \\ C=\left\{ 22;24;26;28 \right\} \\\end{array} \right.\) có 5 số chẵn và 4 số lẻ
Trường hợp 1: Ba số \(A,B,C\) đều là các số lẻ.
Ta cần chọn 3 số lẻ khác nhau từ tập \(L\) làm \(A;B;C\).
Sau đó, các số \(M,N,P\) sẽ được tính theo công thức.
Ta phải kiểm tra xem bộ 6 số tạo thành có phân biệt và đều thuộc \(S\) hay không.
Các bộ 3 số lẻ \(\left\{ A,B,C \right\}\) có thể và các bộ 6 số tương ứng \(\left\{ A,B,C,M,N,P \right\}\(:
\(\left\{ 21,23,27 \right\}\Rightarrow M=22,N=25,P=24\).
Bộ 6 số: \(\left\{ 41,43,47,42,45,44 \right\}\) (thỏa mãn)
\(\left\{ 21,23,29 \right\}\Rightarrow M=22,N=26,P=25\).
Bộ 6 số: \(\left\{ 21,23,29,22,26,25 \right\}\) (thỏa mãn)
\(\left\{ 21,25,27 \right\}\Rightarrow M=23,N=26,P=24\).
Bộ 6 số: \(\left\{ 21,25,27,23,26,44 \right\}\) (thỏa mãn)
\(\left\{ 21,27,29 \right\}\Rightarrow M=24,N=28,P=25\).
Bộ 6 số: \(\left\{ 21,27,29,24,28,25 \right\}\) (thỏa mãn)
\(\left\{ 23,25,29 \right\}\Rightarrow M=24,N=27,P=26\).
Bộ 6 số: \(\left\{ 23,25,29,24,27,26 \right\}\) (thỏa mãn)
\(\left\{ 23,27,29 \right\}\Rightarrow M=25,N=28,P=26\).
Bộ 6 số: \(\left\{ 23,27,29,25,28,26 \right\}\) (thỏa mãn)
Lưu ý: Các bộ như \(\left\{ 21,23,25 \right\}\) sẽ bị loại vì \(P=\frac{\left( 21+25 \right)}{2}=23\), trùng với \(B\).
Trường hợp 2: Ba số \(A,B,C\) đều là các số chẵn.
Ta cần chọn 3 số chẵn khác nhau từ tập \(C\) làm \(A;B;C\).
\(\left\{ 22,24,28 \right\}\Rightarrow M=23,N=26,P=45\).
Bộ 6 số: \(\left\{ 22,24,28,23,26,25 \right\}\) (thỏa mãn)
\(\left\{ 22,26,28 \right\}\Rightarrow M=24,N=27,P=25\).
Bộ 6 số: \(\left\{ 22,26,28,24,27,25 \right\}\) (thỏa mãn)
Lưu ý: Các bộ như \(\left\{ 22,24,26 \right\}\) sẽ bị loại vì \(P=\frac{\left( 22+26 \right)}{2}=24\), trùng với \(B\).
Vậy có 2 bộ số thỏa mãn trong trường hợp này nên có \(6+2=8\) bộ 6 số thỏa mãn yêu cầu.
Với mỗi bộ 6 số hợp lệ, ta đã xác định được đâu là 3 số ở các đỉnh \(\left( A;B;C \right)\) và đâu là 3 số ở các cạnh \(\left( M;N;P \right)\).
Ta có thể hoán vị 3 số ở các đỉnh \(\left( A;B;C \right)\) nên cách hoán vị là \(3!=6\) cách.
Khi 3 giá trị \(\left( A;B;C \right)\) đã được gán, các giá trị \(\left( M;N;P \right)\) sẽ được xác định duy nhất theo công thức.
Ví dụ: Với bộ \(\left\{ 21,23,27,22,25,24 \right\}\) thì nếu ta xếp \(A=21;B=23;C=27\) thì bắt buộc giá trị của ba số lần lượt là: \(M=22;N=25;P=24\).
Số cách xếp thuận lợi là: \(n\left( A \right)=8.3!=8.6=48\) (cách)
nên \(P\left( A \right)=\frac{n\left( A \right)}{n\left( \Omega \right)}=\frac{48}{60480}=\frac{1}{1260}\).
Vậy giá trị của biểu thức \(\frac{2}{a}=\frac{2}{\frac{1}{1260}}=2.1260=2520\).
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Đề Thi Tốt Nghiệp THPT Quốc Gia Năm 2025 - Toán có cấu trúc bám sát theo ma trận kiến thức của Bộ GD-ĐT. Ngoài ra, đề cũng xuất hiện nhiều bài toán thực tế có gắn liền với cuộc sống. Trong đề có 12 câu trắc nghiệm nhiều phương án trả lời bao quát kiến thức lớp 11, 12; 4 câu trắc nghiệm Đúng – Sai cũng thuộc chương trình 12 và 6 câu trắc nghiệm trả lời ngắn bao quát kiến thức lớp 10, 11 và 12. Các chuyên đề trọng điểm như hàm số, đạo hàm, tích phân, phương trình bậc hai, hình học không gian, tổ hợp - xác suất, số phức và phương pháp tọa độ được đưa vào đầy đủ trong đề thi.
Câu hỏi liên quan

Bộ 50 Đề Thi Thử Tốt Nghiệp THPT Giáo Dục Kinh Tế Và Pháp Luật Năm 2026 – Theo Cấu Trúc Đề Minh Họa Bộ GD&ĐT

Bộ 50 Đề Thi Thử Tốt Nghiệp THPT Lịch Sử Học Năm 2026 – Theo Cấu Trúc Đề Minh Họa Bộ GD&ĐT

Bộ 50 Đề Thi Thử Tốt Nghiệp THPT Công Nghệ Năm 2026 – Theo Cấu Trúc Đề Minh Họa Bộ GD&ĐT

Bộ 50 Đề Thi Thử Tốt Nghiệp THPT Môn Hóa Học Năm 2026 – Theo Cấu Trúc Đề Minh Họa Bộ GD&ĐT

Bộ 50 Đề Thi Thử Tốt Nghiệp THPT Môn Sinh Học Năm 2026 – Theo Cấu Trúc Đề Minh Họa Bộ GD&ĐT