10 Đề thi kiểm tra giữa HK1 môn Toán lớp 10 - KNTT - Đề 3
22 câu hỏi 60 phút
Cho \(A,\,\,B\) là hai tập hợp được minh họa như hình vẽ. Phầnkhông bị gạch trong hình vẽ là tập hợp nào sau đây?

\(B\backslash A\)
\(A \cup B\)
\(A \cap B\)
\(A\backslash B\)
Phần không bị gạch trong hình vẽ là tập hợp \(B\backslash A\).
Danh sách câu hỏi:
Phần không bị gạch trong hình vẽ là tập hợp \(B\backslash A\).
Áp dụng công thức Heron: \(S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \) trong đó p là nửa chu vi; \(a,\,b,\,c\) là độ dài các cạnh của tam giác.
Nửa chu vi tam giác ABC là: \(\left( {3 + 5 + 6} \right):2 = 7\).
Diện tích tam giác ABC là:
\({S_{ABC}} = \sqrt {p\left( {p - BC} \right)\left( {p - AC} \right)\left( {p - AB} \right)} = \sqrt {7.\left( {7 - 5} \right).\left( {7 - 6} \right).\left( {7 - 3} \right)} = \sqrt {56} \).
\(\left\{ \begin{array}{l}x > 5\\y + 2 < 0\\x + y \ge 100\end{array} \right.\) là hệ bất phương trình bậc nhất hai ẩn.
\(\begin{array}{*{20}{l}}M&{ = \left( {1 - {\rm{si}}{{\rm{n}}^2}x} \right){\rm{co}}{{\rm{t}}^2}x + 1 - {\rm{co}}{{\rm{t}}^2}x}\\{}&{ = {\rm{co}}{{\rm{t}}^2}x - {\rm{co}}{{\rm{s}}^2}x + 1 - {\rm{co}}{{\rm{t}}^2}x}\\{}&{ = - {\rm{co}}{{\rm{s}}^2}x + 1}\\{}&{ = - {\rm{co}}{{\rm{s}}^2}x + \left( {{\rm{co}}{{\rm{s}}^2}x + {\rm{si}}{{\rm{n}}^2}x} \right)}\\{}&{ = {\rm{si}}{{\rm{n}}^2}x.}\end{array}\)
Ta có: \(\widehat {ABC} = {180^ \circ } - \widehat {BAC} - \widehat {BCA} = {60^ \circ }\).
Áp dụng định lí sin trong \({\rm{\Delta }}ABC\) ta có:
\(\frac{{AC}}{{{\rm{sin}}B}} = \frac{{AB}}{{{\rm{sin}}C}}\)\( \Rightarrow \frac{{50}}{{{\rm{sin}}{{60}^ \circ }}} = \frac{{AB}}{{{\rm{sin}}{{50}^ \circ }}}\)\( \Rightarrow AB \approx 44\) (m).
Câu 13:
Cho góc \(\alpha ,\,\,({90^ \circ } < \alpha < {180^ \circ })\) thỏa mãn \({\rm{sin}}\alpha = m\,\,(0 < m < 1)\)
\({\rm{cos}}\alpha > 0\)
\({\rm{cos}}\alpha = \sqrt {1 - {m^2}} \)
\({\rm{sin}}\left( {{{180}^ \circ } - \alpha } \right) = m\)
\({\rm{ta}}{{\rm{n}}^2}\alpha .{\rm{si}}{{\rm{n}}^2}\alpha - {\rm{ta}}{{\rm{n}}^2}\alpha + {\rm{si}}{{\rm{n}}^2}\alpha - {\rm{sin}}\alpha = 1 - m\)
Câu 14:
Cho hai tập hợp: \(A = \{ x \in \mathbb{R}\mid - 2 < x \le 5\} \), \(B = \{ x \in \mathbb{R}\mid x > 1\} \)
\(A = ( - 2;5{\rm{]}},\,B = \left( {1; + \infty } \right)\)
\(A \cap B = \left( {1;\,5} \right)\)
\(A \cup B = \left[ { - 2;\, + \infty } \right)\)
\({C_\mathbb{R}}\left( {A \cap B} \right) = ( - \infty ;1{\rm{]}} \cup \left( {5; + \infty } \right)\)
Câu 15:
Hưởng ứng phong trào ủng hộ đồng bào miền Bắc vùng bị lũ lụt do cơn bão YAGI gây ra vào đầu tháng 9 vừa qua, bạn Bình được mẹ cho \(250\,000\) đồng mua vở và bút ủng hộ các bạn học sinh vùng lũ. Bình mang \(250\,000\) đồng đi nhà sách để mua một số vở viết và bút. Biết rằng giá một quyển vở viết là \(8\,000\) đồng và giá của một cây bút là \(5\,000\) đồng. Gọi x và y \(\left( {x,\,y \in \mathbb{N}} \right)\) lần lượt là số vở viết và số bút Bình mua được ở nhà sách
Số tiền mua vở viết là \(8x\) (nghìn đồng), số tiền mua bút là \(5y\) (nghìn đồng)
Để Bình trả đủ tiền mua bút và vở viết thì ta có bất phương trình bậc nhất hai ẩn \(x,\,y\) là \(8x + 5y \le 250\)
Với số tiền mẹ cho, Bình có thể mua được 20 quyển vở và 20 chiếc bút để đem ủng hộ
Nếu Bình đã mua 20 chiếc bút thì Bình có thể mua tối đa 19 quyển vở
Câu 16:
Cho tam giác ABC, biết \(BC = 8,\,CA = 6,\,\hat C = {60^ \circ }\)
\(AB \approx 7,20\) (kết quả làm tròn đến hàng phần trăm)
Góc A là góc tù
Bán kính đường tròn nội tiếp tam giác ABC xấp xỉ bằng \(1,96\) (kết quả làm tròn đến hàng phần trăm)
Gọi G là trọng tâm tam giác ABDiện tích tam giác ABG bằng \(4\sqrt 3 \)
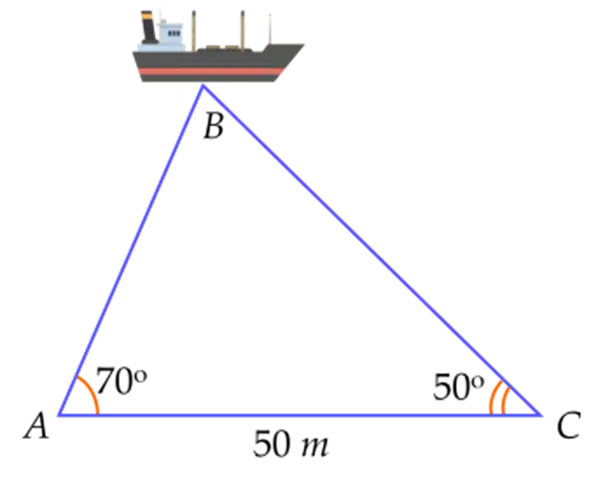 Khoảng cách AB gần bằng
Khoảng cách AB gần bằng
