10 Đề thi kiểm tra giữa HK1 môn Toán lớp 10 - KNTT - Đề 5
22 câu hỏi 60 phút
Phát biểu nào dưới đây không là một mệnh đề Toán học?
Nhà văn Nam Cao quê ở Hà Nam
Số 6 chia hết cho 2
11 là số nguyên tố
2 là số nguyên âm
"Nhà văn Nam Cao quê ở Hà Nam" không là một mệnh đề Toán học.
Danh sách câu hỏi:
"Nhà văn Nam Cao quê ở Hà Nam" không là một mệnh đề Toán học.
\(A = \left\{ {1;2;3;4;5} \right\},\,B = \left\{ {4;5;6} \right\}\) thì
\(A \cap B = \left\{ {4;5} \right\}\) và \(A \cup B = \left\{ {1;2;3;4;5;6} \right\}\).
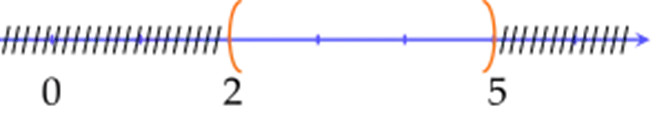
Phần không bị gạch trên trục số biểu diễn tập hợp \(\left( {2;5} \right)\).
\(3x - 2y \ge 6\) là bất phương trình bậc nhất hai ẩn.
Thay các giá trị đã cho và hệ bất phương trình, ta thấy \(N\left( {0; - 2} \right)\) thỏa mãn.
Câu 6:
Hệ thức nào dưới đây đúng?
Câu 13:
Cho mệnh đề P : "Tam giác ABC vuông tại A " và mệnh đề Q : "Tam giác ABC có \(A{B^2} + A{C^2} = B{C^2}\) ". Xét mệnh đề kéo theo \(P \Rightarrow Q\)
Mệnh đề \(P \Rightarrow Q\) được phát biểu là: "Nếu tam giác ABC vuông tại A thì tam giác ABC có \(A{B^2} + A{C^2} = B{C^2}\) "
P là điều kiện cần để có Q
Mệnh đề \(P \Rightarrow Q\) là mệnh để đúng
Mệnh đề đảo của mệnh đề \(P \Rightarrow Q\) là mệnh đề sai
Câu 14:
Nửa mặt phẳng không bị gạch (không kể d) ở hình vẽ dưới đây là miền nghiệm của một bất phương trình bậc nhất hai ẩn.
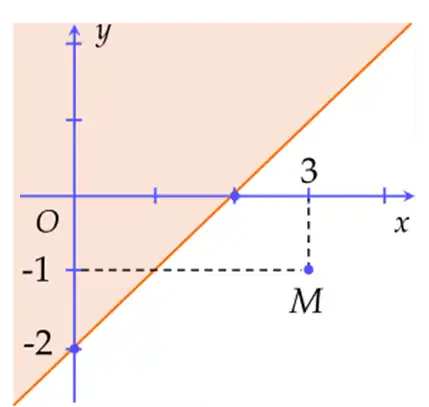
Đường thẳng d đi qua hai điểm có tọa độ \(\left( {2;0} \right)\) và \(\left( {0; - 2} \right)\)
Phương trình của đường thẳng d là \(x - y - 2 = 0\)
Điểm \(M\left( {3; - 1} \right)\) thuộc miền nghiệm của bất phương trình
Nửa mặt phẳng không bị gạch (không kể d ) là miền nghiệm của bất phương trình \(x - y - 2 \ge 0\)
Câu 15:
Cho tam giác ABC có \(\hat A\) là góc tù và thỏa mãn \({\rm{sin}}A = \frac{2}{3}\)
\({\rm{sin}}\left( {B + C} \right) = \frac{2}{3}\)
\({\rm{cos}}A = \frac{{\sqrt 5 }}{3}\)
\({\rm{cot}}\frac{{A + C}}{2} = {\rm{tan}}\frac{B}{2}\)
\({\rm{tan}}\left( {B + C} \right) = - \frac{2}{{\sqrt 5 }}\)
Câu 16:
Cho tam giác ABGọi M là trung điểm của AB, N là điểm thuộc đoạn AC sao cho \(CN = 2AN\), K là trung điểm của MN (tham khảo hình vẽ).
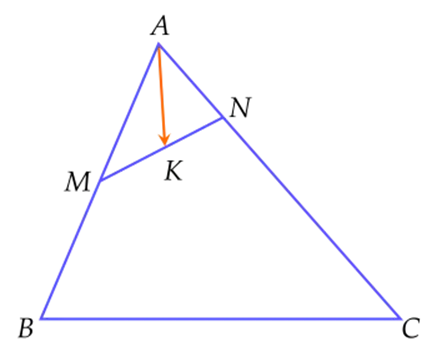
\(\overrightarrow {MA} + \overrightarrow {MB} = \vec 0\)
\(\overrightarrow {CN} = 2\overrightarrow {AN} \)
\(\overrightarrow {OM} + \overrightarrow {ON} = 2\overrightarrow {KO} \) với O là một điểm bất kì
\(\overrightarrow {AK} = \frac{1}{4}\overrightarrow {AB} + \frac{1}{6}\overrightarrow {AC} \)