10 Đề thi kiểm tra giữa HK1 môn Toán lớp 10 - KNTT - Đề 1
22 câu hỏi 60 phút
Mệnh đề phủ định của mệnh đề \(Q:\exists \,x \in \mathbb{R},\,2{x^2} - 5 > 0\) là
\(\bar Q:\exists \,x \in \mathbb{R},\,2{x^2} - 5 = 0\)
\(\bar Q:\forall x \in \mathbb{R},\,2{x^2} - 5 \le 0\)
\(\bar Q:\exists \,x \in \mathbb{R},\,2{x^2} - 5 \le 0\)
\(\bar Q:\forall x \in \mathbb{R},\,2{x^2} - 5 < 0\)
Mệnh đề phủ định của mệnh đề \(Q:\exists \,x \in \mathbb{R},\,2{x^2} - 5 > 0\) là:
\(\bar Q:\forall x \in \mathbb{R},\,2{x^2} - 5 \le 0\).
Danh sách câu hỏi:
Mệnh đề phủ định của mệnh đề \(Q:\exists \,x \in \mathbb{R},\,2{x^2} - 5 > 0\) là:
\(\bar Q:\forall x \in \mathbb{R},\,2{x^2} - 5 \le 0\).
\(I = \{ x \in \mathbb{R}\,|\,x < 1\} = \left( { - \infty ;1} \right)\).
\(A \cup B = \left[ { - 5;2} \right)\).
Tập hợp này có các giá trị nguyên âm là: \(\{ - 5; - 4; - 3; - 2; - 1\}\).
Thay các cặp giá trị vào hệ bất phương trình ta thấy \(\left( {0;\,0} \right)\) thỏa mãn.
Áp dụng định lí côsin, ta có:
\(B{C^2} = A{B^2} + A{C^2} - 2AB.AC.{\rm{cos}}\hat A\)\( = {2^2} + {3^2} - 2.3.{\rm{cos}}{60^ \circ } = 7\).
\( \Rightarrow BC = \sqrt 7 \).
Câu 6:
Tam giác ABC có \(BC = 5\sqrt 5 ,\,AC = 5\sqrt 2 ,\,AB = 5\). Giá trị của \(\widehat {BAC}\) là
Câu 10:
Cho tam giác ABC có \(AB = 8,\,AC = 9\) và \(\hat A = {60^ \circ }\). Diện tích tam giác ABC bằng
Câu 13:
Cho mệnh đề chứa biến \(P\left( x \right):\) " \({x^3} > x\) ''
\(P\left( 1 \right)\) đúng
\(P\left( { - \frac{1}{3}} \right)\) đúng
\(\forall \,x \in \mathbb{N},\,P\left( x \right)\) đúng
\(\exists \,x \in \mathbb{N},\,P\left( x \right)\) đúng
Câu 14:
Cho hai tập hợp \(A = \{ x \in \mathbb{R}\,| - 9 \le x < 3\} \) và \(B = ( - \infty ;3{\rm{]}}\)
\(A = \left[ { - 9;3} \right)\)
\(A \subset B\)
\(B\backslash A = \emptyset \)
\({C_\mathbb{R}}\left( {A \cup B} \right) \cap \mathbb{N} = \left\{ {0;1;2;3} \right\}\)
Câu 15:
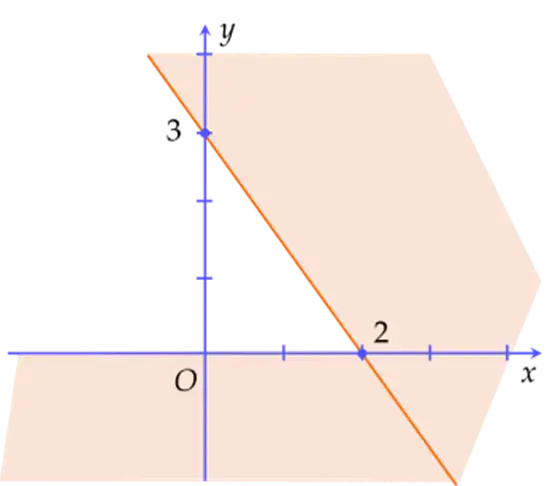
Cho hệ bất phương trình \(\left\{ \begin{array}{l}2x + 5y \ge 30\\2x + y \ge 14\\0 \le x \le 10\\0 \le y \le 9\end{array} \right.\,\,\,\left( I \right)\)
Hệ (I) là một hệ bất phương trình bậc nhất hai ẩn
\(\left( {2;6} \right)\) là một nghiệm của hệ bất phương trình
Miền nghiệm của hệ bất phương trình trên là một miền tam giác
Biểu thức \(F\left( {x;y} \right) = 4x + 3y\) với (x;y) là nghiệm của hệ bất phương trình đã cho đạt giá trị nhỏ nhất tại điểm \(\left( {{x_0};{y_0}} \right)\). Khi đó \({y_0} - {x_0} = - 1\)
Câu 16:
Cho \({\rm{cos}}\alpha = \frac{1}{3}\) với \({0^ \circ } < \alpha < {90^ \circ }\)
Giá trị \({\rm{sin}}\alpha .{\rm{cos}}\alpha < 0\)
Có \({\rm{sin}}\alpha = \frac{{2\sqrt 2 }}{3}\)
Có \({\rm{tan}}\alpha = \frac{{\sqrt 2 }}{4}\)
Giá trị biểu thức \(\frac{{6\sqrt 2 {\rm{sin}}\alpha + 3{\rm{cos}}\alpha }}{{\sqrt 2 {\rm{tan}}\alpha + 2\sqrt 2 {\rm{cot}}\alpha }}\) bằng \(\frac{9}{5}\)