10 Đề thi kiểm tra cuối HK1 môn Toán lớp 10 - CTST - Đề 1
21 câu hỏi 60 phút
Cho tập hợp \(A = \left\{ {1;2;3;4;5} \right\}\). Số tập con có hai phần tử của A là
10
5
20
15
Các tập con có 2 phần tử của tập hợp A là:
\(\left\{ {1;2} \right\},\left\{ {1;3} \right\},\left\{ {1;4} \right\},\left\{ {1;5} \right\},\left\{ {2;3} \right\},\left\{ {2;4} \right\},\left\{ {2;5} \right\},\left\{ {3;4} \right\},\left\{ {3;5} \right\},\left\{ {4;5} \right\}\).
Vậy có 10 tập con có hai phần tử của tập hợp A.
Danh sách câu hỏi:
Các tập con có 2 phần tử của tập hợp A là:
\(\left\{ {1;2} \right\},\left\{ {1;3} \right\},\left\{ {1;4} \right\},\left\{ {1;5} \right\},\left\{ {2;3} \right\},\left\{ {2;4} \right\},\left\{ {2;5} \right\},\left\{ {3;4} \right\},\left\{ {3;5} \right\},\left\{ {4;5} \right\}\).
Vậy có 10 tập con có hai phần tử của tập hợp A.
\(X \cup Y = \left\{ { - 1;0;1;2;4;7;9;10} \right\}\). Tập hợp \(X \cup Y\) có 8 phần tử.
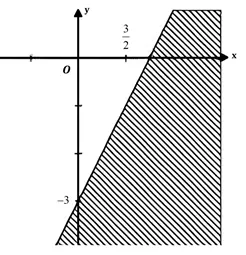
Dựa vào đồ thị hàm số ta có đường thẳng đi qua hai điểm \(\left( {\frac{3}{2};0} \right)\) và \(\left( {0; - 3} \right)\) là \(2x - y = 3\).
Điểm \(O\left( {0;0} \right)\) thuộc miền nghiệm của bất phương trình và \(2.0 - 0 \le 3\) nên nửa mặt phẳng không gạch là miền nghiệm của bất phương trình \(2x - y \le 3\).
Thay tọa độ điểm \(M\left( {1;1} \right)\) vào hệ bất phương trình ta thấy thỏa mãn hệ. Do đó điểm \(M\left( {1;1} \right)\) thuộc miền nghiệm của hệ bất phương trình.
Điều kiện: \(x - 1 > 0 \Leftrightarrow x > 1\).
Vậy tập xác định của hàm số là \(D = \left( {1; + \infty } \right)\).
Câu 8:
Cho tam giác ABC có bán kính đường tròn ngoại tiếp tam giác là R. Khẳng định nào dưới đây đúng?
Câu 10:
Cho tam giác ABC, gọi M là trung điểm của BC và G là trọng tâm của tam giác ABCâu nào sau đây đúng?
Câu 13:
Cho hàm số bậc hai \(y = f\left( x \right) = a{x^2} + bx + c\) có đồ thị như hình vẽ:
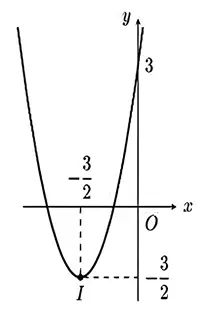
Đồ thị hàm số có trục đối xứng \(x = - \frac{3}{2}\)
Giá trị lớn nhất của hàm số là \( - \frac{3}{2}\)
Phương trình \(f\left( x \right) = 0\) có 2 nghiệm phân biệt
\(a > 0;b < 0;c > 0\)
Câu 14:
Điểm trung bình môn học kì I của hai bạn An và Bình được cho như bảng:
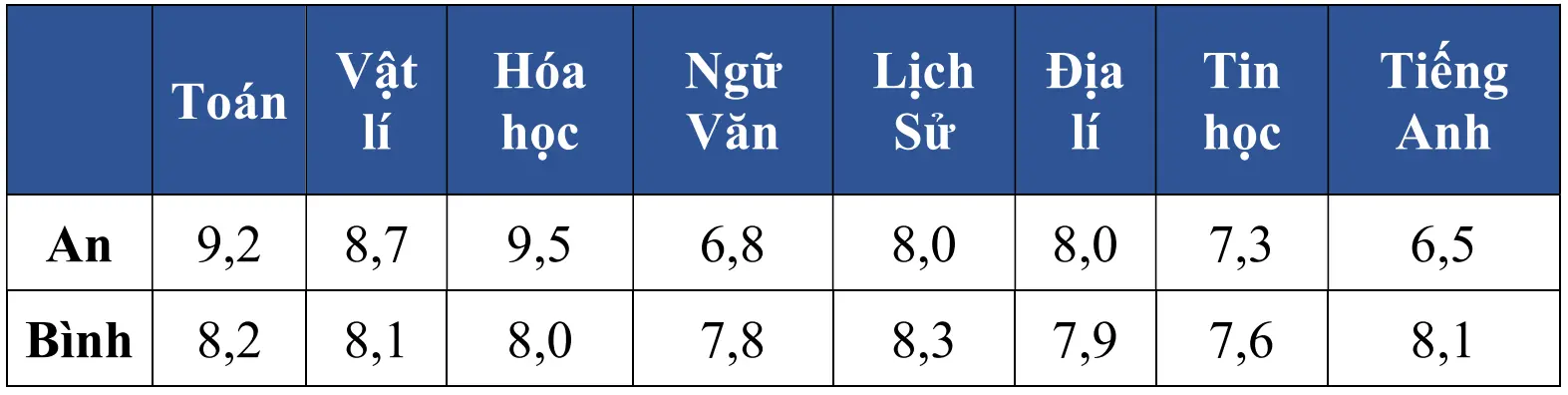
Xét tính đúng/sai của các mệnh đề sau:
Khoảng biến thiên điểm của bạn An là \({R_1} = 0,7\)
Bạn An học đều hơn bạn Bình
Điểm trung bình môn học kì I của bạn Bình là 8,0
Phương sai của mẫu số liệu về điểm trung bình học kỳ I của bạn An là 1,022