10 Đề thi kiểm tra cuối HK1 môn Toán lớp 10 - CTST - Đề 2
21 câu hỏi 60 phút
Điểm nào dưới đây thuộc miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{2x - 2y \le 3}\\{2x + y > - 2}\end{array}} \right.\) ?
\(\left( {1; - 2} \right)\)
\(\left( {0; - 3} \right)\)
\(\left( { - 1; - 2} \right)\)
\(\left( {1;1} \right)\)
Thay tọa độ các điểm vào hệ bất phương trình ta được điểm \(\left( {1;1} \right)\) thuộc miền nghiệm của bất phương trình đã cho.
Danh sách câu hỏi:
Thay tọa độ các điểm vào hệ bất phương trình ta được điểm \(\left( {1;1} \right)\) thuộc miền nghiệm của bất phương trình đã cho.
\(\overrightarrow {AB} = - 2\overrightarrow {CA} \) \( \Rightarrow \overrightarrow {AB} = 2\overrightarrow {AC} \).
Từ đây ta có C là trung điểm của AB.

Trong dãy số liệu giá trị lớn nhất là 32 và giá trị nhỏ nhất là 21.
Vậy khoảng biến thiên là: \(R = 32 - 21 = 11\).
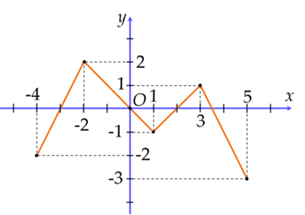
Từ đồ thị ta thấy \({\rm{max}}f\left( x \right) = 2 = M\) và \({\rm{min}}f\left( x \right) = - 3 = m\).
Vậy \(M - m = 2 - \left( { - 3} \right) = 5\).
\(A = {C_\mathbb{R}}\left( { - \infty ;2} \right) = \left[ {2; + \infty } \right)\).

Khi đó \(A\backslash B = \left( {3; + \infty } \right)\).
Câu 13:
Cho hệ bất phương trình \(\left( I \right):\left\{ {\begin{array}{*{20}{c}}{20 \le y \le 4}\\{x \ge 0}\\{x - y \le 1}\\{x + 2y \le 10}\end{array}} \right.\). Xét tính đúng/sai của các mệnh đề sau:
Miền nghiệm của hệ bất phương trình (I) chứa điểm \(M\left( {1;2} \right)\)
Điểm \(N\left( {2;3} \right)\) không thuộc miền nghiệm của hệ bất phương trình (I)
Miền nghiệm của hệ bất phương trình (I) là miền ngũ giác OABCD (phần ngũ giác được tô đậm) trong hình vẽ sau.
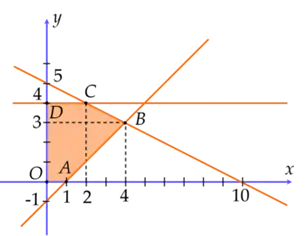
Biểu thức \(F\left( {x;y} \right) = x - 2y\) với \(\left( {x:y} \right)\) thỏa mãn hê bất phương trình (I) đat giá trị nhỏ nhất khi \(x = 2,\,y = 4\)
Câu 14:
Cho hình vuông ABCD cạnh bằng a (Hình vẽ).

Xét tính đúng/sai của các mệnh đề sau:
\(\overrightarrow {BC} + \overrightarrow {BA} = \overrightarrow {BD} \)
Độ dài của vectơ \(\overrightarrow {AB} + \overrightarrow {CB} \) bằng \(2a\)
\(\overrightarrow {BA} .\overrightarrow {DB} = - {a^2}\)
Với điểm M bất kì, cho biểu thức \(T = \left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} } \right|\). Giá trị nhỏ nhất của T là \(2025a\)