10 Đề thi kiểm tra cuối HK1 môn Toán lớp 10 - CTST - Đề 3
21 câu hỏi 60 phút
Cho \(\vec a\) và \(\vec b\) là hai vectơ ngược hướng và đều khác vectơ \(\vec 0\). Khẳng định nào sau đây đúng?
\(\vec a.\,\vec b = \left| {\vec a\left| . \right|\vec b} \right|\)
\(\left( {\vec a,\,\vec b} \right) = {0^0}\)
\(\vec a,\,\vec b = 0\)
\(\left( {\vec a,\,\vec b} \right) = {180^ \circ }\)
\(\vec a\) và \(\vec b\) ngược hướng thì \(\left( {\vec a,\,\vec b} \right) = {180^ \circ }\).
Danh sách câu hỏi:
\(\vec a\) và \(\vec b\) ngược hướng thì \(\left( {\vec a,\,\vec b} \right) = {180^ \circ }\).
Ta có \(\left( {\overrightarrow {AB} ,\,\overrightarrow {AC} } \right) = \widehat {BAC} = {90^ \circ }\).
Tổng số tiền mua gạo không vượt quá \(300\,000\) đồng nên ta có
\(25\,000x + 20\,000y \le 300.000 \Leftrightarrow 5x + 4y \le 60\).
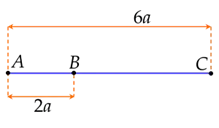
Từ giả thiết ta có \(AC = 3AB\), đồng thời B nằm giữa A và C nên \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) cùng hướng.
Vậy \(\overrightarrow {AC} = 3\overrightarrow {AB} \).
Với \(k \ne 0\) thì \(\left| {k\vec a\left| { = \left| k \right|.} \right|\vec a} \right|\).
Câu 11:
Cho ba điểm phân biệt \(A,\,B,\,C\). Khi đó \(\overrightarrow {CA} + \overrightarrow {AB} \) bằng
Câu 13:
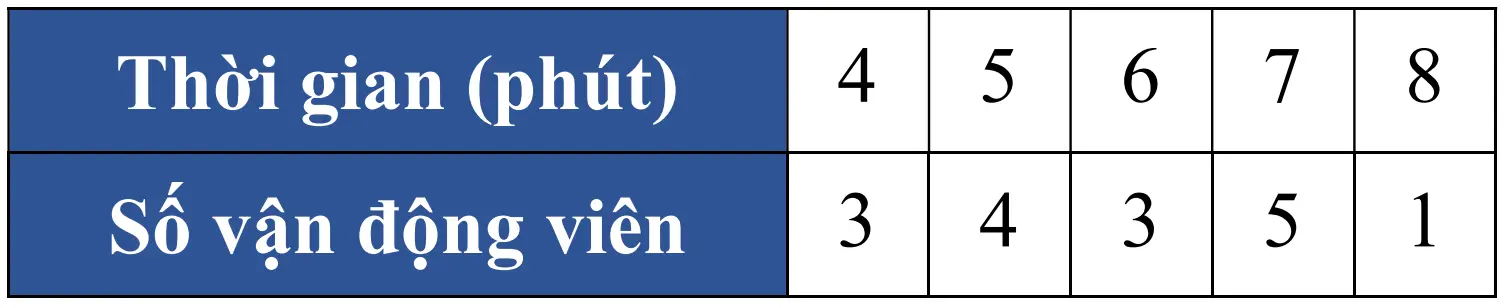
Trong một cuộc thi thể thao, người ta ghi lại thời gian hoàn thành chặng đường đua của một số vận động viên ở bảng sau:
Xét tính đúng/sai của các mệnh đề sau:
Mốt của mẫu số liệu trên là 7
Độ lệch chuẩn (làm tròn đến hàng phần trăm) của mẫu số liệu trên là \(1,23\)
Tứ phân vị thứ nhất và thứ ba của mẫu số liệu trên lần lượt là 5 và 6
Khoảng tứ phân vị của mẫu số liệu trên là 2
Câu 14:
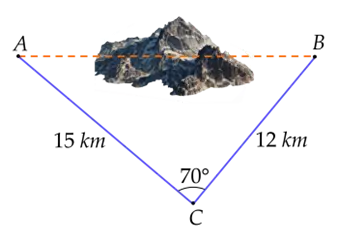
Chùa Ông Núi - ngôi cổ tự linh thiêng danh tiếng ở Bình Định, tọa lạc tại đỉnh Chóp Vung, huyện Phù Cát, tỉnh Bình Định và cách thành phố Quy Nhơn 30 km. Điểm nổi bật nhất của chùa chính là bức tượng Phật ngồi lớn nhất Đông Nam Á.
Để tính chiều cao AB của bức tượng, người ta đo ở hai vị trí C và D cách nhau 200 m. Tại C người ta đo được \(BCE = {52^ \circ },\,ACE = {67^ \circ }\) tại D người ta đo được \(BDC = {23^ \circ }\) (như hình vẽ).

Xét tính đúng/sai của các mệnh đề sau:
\(\widehat {CBD} = {29^ \circ }\)
Độ dài cạnh BC (làm tròn đến hàng đơn vị) là 162 m
\(\widehat {BAC} = {24^ \circ }\)
Chiều cao của bức tượng (làm tròn đến hàng đơn vị) là 107 m
Câu 19:
Cho đồ thị hàm số \(y = 2{x^2} + 6x + 5\). Xét tính đúng/sai của các mệnh đề sau:
Đỉnh là \(I\left( { - \frac{3}{2};\frac{1}{2}} \right)\)
Đồ thị của hàm số là:
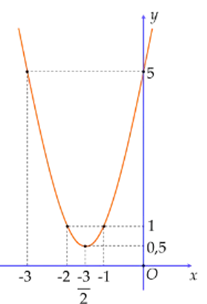
Hàm số nghịch biến trên khoảng \(\left( { - \infty ; - \frac{3}{2}} \right)\)
Hàm số đồng biến trên khoảng \(\left( { - \frac{3}{2}; + \infty } \right)\)