Câu hỏi:
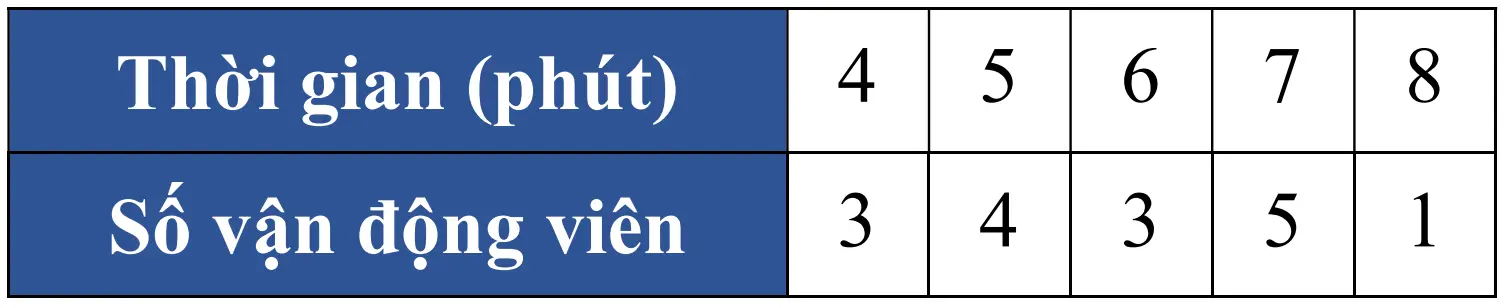
Trong một cuộc thi thể thao, người ta ghi lại thời gian hoàn thành chặng đường đua của một số vận động viên ở bảng sau:
Xét tính đúng/sai của các mệnh đề sau:
Đáp án đúng: Đúng, Sai, Sai, Đúng
a) Đúng.
Vì giá trị 7 có tần số lớn nhất (bằng 5) nên \({M_0} = 7\).
b) Sai.
Tổng số vận động viên là \(n = 3 + 4 + 3 + 5 + 1 = 16\).
Số trung bình của mẫu số liệu là:
\(\bar x = \frac{{3.4 + 4.5 + 3.6 + 5.7 + 8}}{{16}} = 5,8125\).
Phương sai của mẫu số liệu là:
\({s^2} = \frac{{\left[ \begin{array}{l}3{(4 - 5,8125)^2} + 4{(5 - 5,8125)^2} + 3{(6 - 5,8125)^2}\\ + 5{(7 - 5,8125)^2} + {(8 - 5,8125)^2}\end{array} \right]}}{{16}} = \frac{{391}}{{256}}\).
Độ lệch chuẩn của mẫu số liệu là:
\(s = \sqrt {\frac{{391}}{{256}}} \approx 1,24\).
c) Sai + d) Đúng.
Gọi \({x_1},\,{x_2},\, \ldots ,\,{x_{16}}\) là thời gian của các vận động viên được sắp xếp theo thứ tự không giảm.
Vì cỡ mẫu \(n = 16\) là số chẵn nên trung vị của mẫu số liệu là trung bình cộng của giá trị \({x_8}\) và \({x_9}\) như trong bảng số liệu.
Ta thấy hai giá trị này đều bằng 6.
Suy ra \({M_e} = \frac{{6 + 6}}{2} = 6\).
• Xét dãy số liệu từ \({x_1}\) đến \({x_8}\).
Tứ phân vị thứ nhất là trung vị của dãy số liệu này và \({Q_1} = \frac{{{x_4} + {x_5}}}{2} = 5\).
• Xét dãy số liệu từ \({x_9}\) đến \({x_{16}}\).
Tứ phân vị thứ ba là trung vị của dãy số liệu này và \({Q_3} = \frac{{{x_{12}} + {x_{13}}}}{2} = 7\).
Vậy khoảng tứ phân vị là: \({{\rm{\Delta }}_Q} = {Q_3} - {Q_1} = 7 - 5 = 2\).
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Bộ Đề Kiểm Tra Học Kì I - Toán 10 - Chân Trời Sáng Tạo - Bộ Đề 01 là bài kiểm tra trắc nghiệm online được thiết kế theo cấu trúc mới của Bộ Giáo dục và Đào tạo. Đề thi bao gồm nhiều dạng câu hỏi như: nhiều phương án lựa chọn, đúng sai, trả lời ngắn và tự luận. Mỗi câu hỏi tập trung vào các kiến thức trọng tâm của chương trình Toán lớp 10, giúp học sinh ôn tập và củng cố kiến thức một cách hiệu quả. Đề thi không chỉ kiểm tra khả năng lý thuyết mà còn đánh giá khả năng giải quyết vấn đề thực tế của học sinh.
Câu hỏi liên quan

Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – I-Learn Smart World – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – Global Success – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Kết Nối Tri Thức – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Chân Trời Sáng Tạo – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Công Nghệ 12 – Kết Nối Tri Thức – Năm Học 2025-2026