Câu hỏi:
Bạn Hoa dự định vẽ các tấm thiệp xuân làm bằng tay để bán trong một hội chợ gây quỹ từ thiện. Hoa cần 2 giờ để vẽ một tấm thiệp loại nhỏ có giá 10 nghìn đồng và 3 giờ để vẽ một tấm thiệp loại lớn có giá 20 nghìn đồng. Biết rằng bạn Hoa chỉ có 30 giờ để vẽ và ban tổ chức hội chợ yêu cầu phải vẽ ít nhất 12 tấm. Bạn Hoa có thể thu được số tiền (nghìn đồng) nhiều nhất là bao nhiêu để gây quỹ từ thiện?
Đáp án đúng: 180
Gọi x là số tấm thiệp loại nhỏ và y là số tấm thiệp loại lớn mà bạn Hoa vẽ \(\left( {x,\,y \in \mathbb{N}} \right)\).
Từ giả thiết ta có hệ bất phương trình: \(\left\{ \begin{array}{l}2x + 3y \le 30\\x + y \ge 12\\x \ge 0\\y \ge 0\end{array} \right.\).
Biểu diễn miền nghiệm của hệ bất phương trình trên trên mặt phẳng tọa độ Oxy:
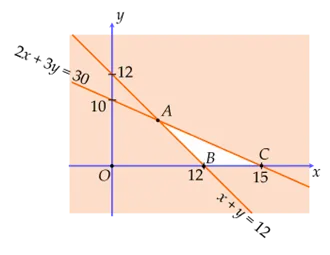
Từ đây ta có miền nghiệm của hệ bất phương trình là miền trong của tam giác ABC (kể cả các cạnh).
Trong đó \(A\left( {6;6} \right),\,B\left( {12;0} \right),\,C\left( {15;0} \right)\).
Giá thiệp nhỏ là 10 nghìn đồng/tấm và giá thiệp lớn là 20 nghìn đồng/tấm.
Khi đó tổng số tiền thu được (đơn vị: nghìn đồng) là:
\(F\left( {x,y} \right) = 10x + 20y\).
Biểu thức F(x, y) đạt giá trị lớn nhất chỉ có thể tại các đỉnh của tam giác ABC.
Ta có:
\(F\left( {6;6} \right) = 10.6 + 20.6 = 180\).
\(F\left( {12;0} \right) = 10.12 + 20.0 = 120\).
\(F\left( {15;0} \right) = 10.15 + 20.0 = 150\).
Suy ra \({\rm{max}}F\left( {x;y} \right) = 180\) khi \(x = 6,\,y = 6\).
Vậy Hoa có thể thu được nhiều nhất 180 (nghìn đồng) nếu làm 6 tấm thiệp lớn và 6 tấm thiệp nhỏ.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Bộ Đề Kiểm Tra Học Kì I - Toán 10 - Chân Trời Sáng Tạo - Bộ Đề 01 là bài kiểm tra trắc nghiệm online được thiết kế theo cấu trúc mới của Bộ Giáo dục và Đào tạo. Đề thi bao gồm nhiều dạng câu hỏi như: nhiều phương án lựa chọn, đúng sai, trả lời ngắn và tự luận. Mỗi câu hỏi tập trung vào các kiến thức trọng tâm của chương trình Toán lớp 10, giúp học sinh ôn tập và củng cố kiến thức một cách hiệu quả. Đề thi không chỉ kiểm tra khả năng lý thuyết mà còn đánh giá khả năng giải quyết vấn đề thực tế của học sinh.
Câu hỏi liên quan

Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – I-Learn Smart World – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – Global Success – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Kết Nối Tri Thức – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Chân Trời Sáng Tạo – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Công Nghệ 12 – Kết Nối Tri Thức – Năm Học 2025-2026