Câu hỏi:
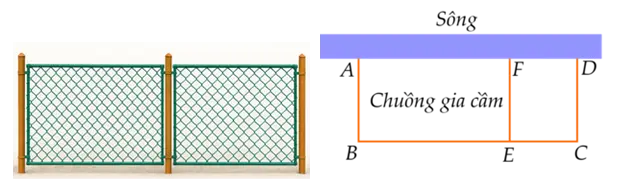
Một chủ trang trại nuôi gia cầm muốn rào một khu đất cạnh bờ sông thành hai chuồng nuôi gia cầm hình chữ nhật sát nhau, một chuồng nuôi gà và một chuồng nuôi vịt (hình vẽ). Biết rằng trang trại đã có sẵn 180 m dài hàng rào và phần chuồng cạnh bờ sông thì không phải rào. Diện tích khu đất được rào lớn nhất là bao nhiêu \({{\rm{m}}^{\rm{2}}}\)?
Đáp án đúng: 2700
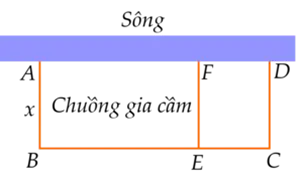
Gọi độ dài cạnh AB là x m \((0 < x < 180)\).
Ta có \(BC = 180 - AB - EF - CD = 180 - 3x\) (m).
Diện tích khu đất được rào là:
\(S = x\left( {180 - 3x} \right) = - 3{x^2} + 180x\left( {{{\rm{m}}^{\rm{2}}}} \right)\).
Xét hàm số \(f\left( x \right) = - 3{x^2} + 180x\) trên khoảng \(\left( {0;180} \right)\).
Hàm số f(x) là một parabbol có hệ số của \({x^2}\) bằng \( - 3 < 0\) nên có bề lõm quay xuống.
Suy ra f(x) đạt giá trị nhỏ nhất tại \(x = - \frac{{180}}{{2.\left( { - 3} \right)}} = 30\).
Do đó \({\rm{max}}f\left( x \right) = f\left( {30} \right) = - {3.30^2} + 180.30 = 2700\).
Vậy diện tích lớn nhất của khu đất là 2700 \({{\rm{m}}^{\rm{2}}}\).
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Bộ Đề Kiểm Tra Học Kì I - Toán 10 - Chân Trời Sáng Tạo - Bộ Đề 01 là bài kiểm tra trắc nghiệm online được thiết kế theo cấu trúc mới của Bộ Giáo dục và Đào tạo. Đề thi bao gồm nhiều dạng câu hỏi như: nhiều phương án lựa chọn, đúng sai, trả lời ngắn và tự luận. Mỗi câu hỏi tập trung vào các kiến thức trọng tâm của chương trình Toán lớp 10, giúp học sinh ôn tập và củng cố kiến thức một cách hiệu quả. Đề thi không chỉ kiểm tra khả năng lý thuyết mà còn đánh giá khả năng giải quyết vấn đề thực tế của học sinh.
Câu hỏi liên quan

Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – I-Learn Smart World – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – Global Success – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Kết Nối Tri Thức – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Chân Trời Sáng Tạo – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Công Nghệ 12 – Kết Nối Tri Thức – Năm Học 2025-2026