10 Đề thi kiểm tra giữa HK1 môn Toán lớp 10 - CTST - Đề 3
22 câu hỏi 60 phút
Cho mệnh đề chứa biến P(x): "\(x+10\ge {{x}^{2}}\) với x là số tự nhiên". Mệnh đề nào sau đây sai?
\(P\left( 3 \right)\)
\(P\left( 1 \right)\)
\(P\left( 4 \right)\)
\(P\left( 2 \right)\)
\(P\left( 1 \right)=11\ge {{1}^{2}}\) là mệnh đề đúng.
\(P\left( 2 \right)=12\ge {{2}^{2}}\) là mệnh đề đúng.
\(P\left( 3 \right)=13\ge {{3}^{2}}=9\) là mệnh đề đúng.
\(P\left( 4 \right)=14\ge {{4}^{2}}=16\) là mệnh đề sai.
Danh sách câu hỏi:
Câu 1:
Cho mệnh đề chứa biến P(x): "\(x+10\ge {{x}^{2}}\) với x là số tự nhiên". Mệnh đề nào sau đây sai?
\(P\left( 1 \right)=11\ge {{1}^{2}}\) là mệnh đề đúng.
\(P\left( 2 \right)=12\ge {{2}^{2}}\) là mệnh đề đúng.
\(P\left( 3 \right)=13\ge {{3}^{2}}=9\) là mệnh đề đúng.
\(P\left( 4 \right)=14\ge {{4}^{2}}=16\) là mệnh đề sai.
Do tất cả các phần tử \(1;3;5;7\) thuộc tập hợp C cũng thuộc tập hợp A nên \(C\subset A\).
Ta có \(X\cup Y=\left\{ -1\,;\,0\,;\,1\,;\,2\,;\,4\,;\,7\,;\,9\,;\,10 \right\}\).
Do đó \(X\cup Y\) có 8 phần tử.
Ta có: \(15<2x+1\le 21\)\(\Leftrightarrow 14<2x\le 20\)\(\Leftrightarrow 7<x\le 10\).
Do đó \(P=\left\{ x\in \mathbb{R}\,|\,15<1+2x\le 21 \right\}=\left( 7;10 \right]\).
Gọi \(I\left( {{x}_{I}};{{y}_{I}} \right)\) là tọa độ đỉnh của parabol (P).
Ta có \(\left\{ \begin{align} & {{x}_{I}}=-\frac{b}{2a}=\frac{1}{3} \\ & {{y}_{I}}=3.{{\left( \frac{1}{3} \right)}^{2}}-2.\frac{1}{3}+1=\frac{2}{3} \\ \end{align} \right.\)
Vậy tọa độ đỉnh của parabol (P) là \(I\left( \frac{1}{3};\frac{2}{3} \right)\).
Câu 6:
Cho tam giác ABC có \(AB=3\), \(BC=5\) và độ dài đường trung tuyến \(BM=\sqrt{13}\).
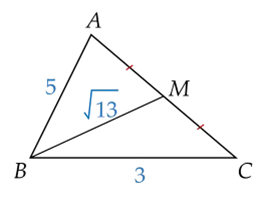
Độ dài AC bằng
Câu 13:
Cho mệnh đề chứa biến \(P\left( x \right):\) '' \(x>{{x}^{3}}\) ". Xét tính đúng/sai của các khẳng định sau
\(P\left( \frac{1}{3} \right)\) là mệnh đề đúng
\(P\left( \frac{1}{3} \right)\) là mệnh đề sai
Với mọi giá trị \(x\in \mathbb{N},\,P\left( x \right)\) không thể xác định tính đúng, sai
\(P\left( 1 \right)\) là mệnh đề sai
Câu 14:
Cho ba tập hợp \({{C}_{\mathbb{R}}}M=\left( -\infty ;3 \right),\,{{C}_{\mathbb{R}}}N=\left( -\infty ;-3 \right)\cup \left( 3;+\infty \right)\) và \({{C}_{\mathbb{R}}}P=\left( -2;3 \right]\). Xét tính đúng/sai của các khẳng định sau
\(\left( M\cap N \right)\cup P=\left( -\infty ;-2 \right]\cup \left[ 3;+\infty \right)\)
\(M\cap N=\varnothing \)
\(N=\left( -3;3 \right)\)
\(P=\left( -\infty ;-2 \right]\cup \left( 3;+\infty \right)\)
Câu 15:
Một đội sản xuất cần 3 giờ để làm xong sản phẩm loại I và 2 giờ để làm xong sản phẩm loại II. Biết thời gian tối đa cho việc sản xuất hai sản phẩm trên là 18 giờ. Gọi \(x,\,y\) lần lượt là số sản phẩm loại I, loại II mà đội làm được trong thời gian cho phép.
Xét tính đúng/sai của các khẳng định sau
\(3x+2y<18\)
Tổng thời gian (giờ) làm xong sản phẩm loại I là \(2x\), tổng thời gian làm xong sản phẩm loại II là \(3y\)
Khi số sản phẩm loại I là 2, loại II là 6 thì thời gian đội đó làm vượt quá thời gian cho phép
Khi số sản phẩm loại I là 3, loại II là 4 thì thời gian đội đó làm nằm trong thời gian cho phép
Câu 16:
Cho \(\text{cos}\alpha =\frac{3}{4}\). Xét tính đúng/sai của các khẳng định sau
\(\text{si}{{\text{n}}^{2}}\alpha =\frac{7}{16}\)
\(A=3\text{si}{{\text{n}}^{2}}\alpha +\text{co}{{\text{s}}^{2}}\alpha =\frac{5}{8}\)
\(B=5\text{si}{{\text{n}}^{2}}\alpha -3\text{co}{{\text{s}}^{2}}\alpha =\frac{1}{2}\)
\(C=\sqrt{\text{si}{{\text{n}}^{2}}\alpha +\text{co}{{\text{s}}^{4}}\alpha }+\sqrt{\text{si}{{\text{n}}^{4}}\alpha +\text{co}{{\text{s}}^{2}}\alpha }=\frac{\sqrt{193}}{9}\)