10 Đề thi kiểm tra giữa HK1 môn Toán lớp 10 - Cánh Diều - Đề 5
21 câu hỏi 60 phút
Mệnh đề "Có một số mà bình phương không âm" viết lại bằng kí hiệu toán học là
"\(\exists \,x \in R\,\,\left| {\,{x^2} > } \right.0\)"
" \(\exists \,x \in R\left| {\,{x^2} \ge } \right.0\) "
" \(\forall \,x \in R\,\left| {\,{x^2} \ge } \right.0\) "
" \(\forall x \in R\,\left| {\,{x^2} > } \right.0\) "
Mệnh đề " Có một số mà bình phương không âm" viết lại bằng kí hiệu toán học là "\(\exists \,x \in R\left| {\,{x^2} \ge } \right.0\)".
Danh sách câu hỏi:
Mệnh đề " Có một số mà bình phương không âm" viết lại bằng kí hiệu toán học là "\(\exists \,x \in R\left| {\,{x^2} \ge } \right.0\)".
\(\left\{ {\begin{array}{*{20}{c}}{2x - y > 4}\\{x - 3y \le 1}\end{array}} \right.\) là hệ bất phương trình bậc nhất hai ẩn.
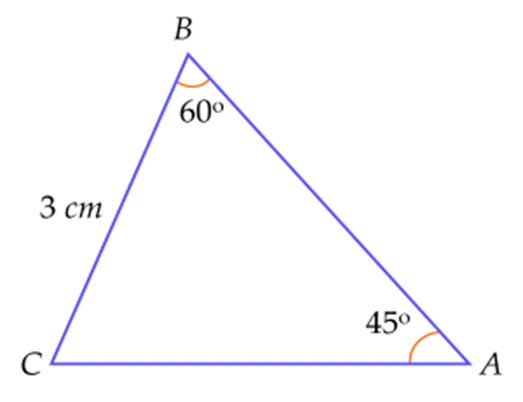
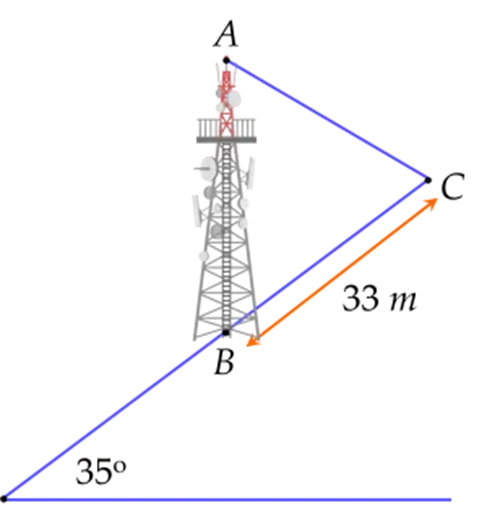
Áp dụng định lí sin, ta có: \(\frac{{BC}}{{{\rm{sin}}\,A}} = \frac{{AC}}{{{\rm{sin}}\,B}}\).
suy ra \(AC = \frac{{3\sqrt 6 }}{2}\).
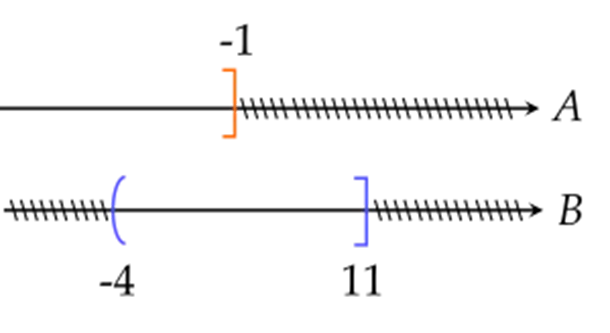
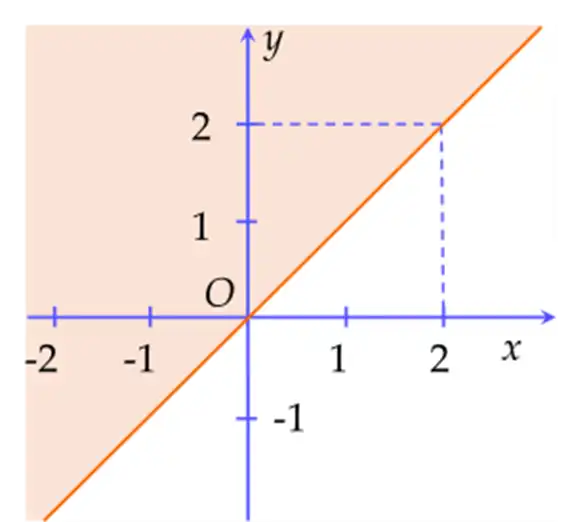
Từ hình vẽ trên, ta thấy \(B\backslash A = ( - 1;11]\).
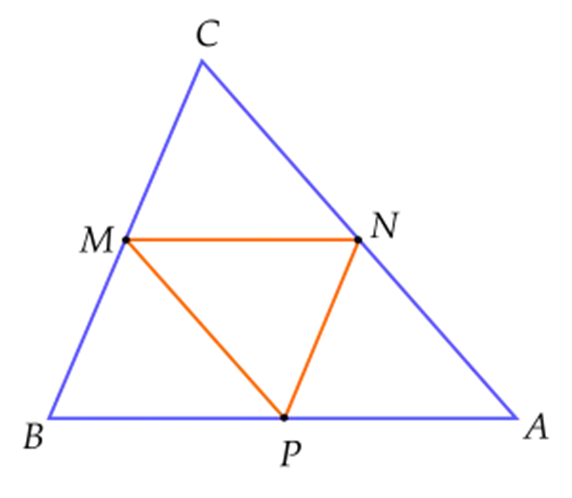
Theo định lí cosin: \(M{N^2} = P{M^2} + P{N^2} - 2PM.PN.{\rm{cos}}\,P\).
Câu 11:
Phát biểu nào dưới đây sai?
Câu 12:
Khẳng định nào sau đây đúng?
Câu 13:
Cho tập \(A = ( - 5;5]\,,\,B = \left( { - 2;8} \right)\) và \(\mathbb{N}\) là tập hợp số tự nhiên
Tập \(B \cap \mathbb{N}\) có 9 phần tử
\(B\backslash A = \left( {5;8} \right)\)
\({C_\mathbb{R}}\left( {A \cup B} \right) = \left[ { - 5;8} \right]\)
\(A \cap B = ( - 2;5]\)
Câu 14:
Cho hình bình hành ABCD có giao điểm của hai đường chéo là O. Gọi \(M,\,N\) lần lượt là trung điểm của \(AB,\,BC\).

\(\overrightarrow {AB} = \overrightarrow {CD} \)
\(\overrightarrow {MN} = \overrightarrow {AO} \)
Tập hợp các điểm K thỏa mãn \(\left| {\overrightarrow {KA} + \overrightarrow {KC} \left| { = 2} \right|\overrightarrow {KB} } \right|\) là đường trung trực của \(OB.\)
\(\left| {\overrightarrow {BA} + \overrightarrow {BC} \left| { = 2} \right|\overrightarrow {BO} } \right|\)