Đề thi thử Tốt nghiệp THPT năm 2025 môn Toán Sở GD&ĐT Thừa Thiên Huế - Đề 3
22 câu hỏi 60 phút
Cho hình chóp \(S.ABC\) có đường thẳng \(SA\) vuông góc với đáy \(\left( ABC \right)\), \(SA=2a\). Khoảng cách từ điểm \(S\) đến đường thẳng \(AB\) bằng:
\(a.\)
\(3a.\)
\(2a.\)
\(\frac{a}{2}.\)
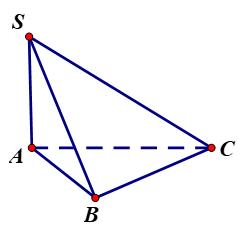
Vì \(SA\) vuông góc với đáy \(\left( ABC \right)\).
nên \(SA\bot AB\Rightarrow d\left( S,AB \right)=SA=2a\).
Danh sách câu hỏi:

Vì \(SA\) vuông góc với đáy \(\left( ABC \right)\).
nên \(SA\bot AB\Rightarrow d\left( S,AB \right)=SA=2a\).
Ta có \({f}'\left( 2 \right)=\underset{x\to 2}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( 2 \right)}{x-2}=3\).
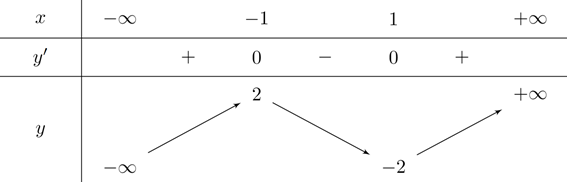
Dựa vào bảng biến thiên ta có giá trị nhỏ nhất của hàm số \(y=f\left( x \right)\) trên \(\left[ -1\,;\,1 \right]\) bằng \(-2\).
Ta có \(\left\{ \begin{align} & BC\bot SA \\ & BC\bot AB \\ \end{align} \right.\Rightarrow BC\bot \left( SAB \right)\).
Ta có \({A}'A\bot \left( ABCD \right)\) nên \(d\left( {A}',\left( ABCD \right) \right)={A}'A=a\).
Câu 13:
Một bệnh nhân hàng ngày phải uống \(150mg\) thuốc kháng sinh đặc trị bệnh bạch hầu. Sau một ngày hàm lượng thuốc kháng sinh đặc trị bệnh bạch hầu trong cơ thể vẫn còn \(6%\) lượng thuốc của ngày hôm trước.
Các mệnh đề sau đúng hay sai?
Lượng thuốc kháng sinh đặc trị bệnh bạch hầu còn trong cơ thể sau ngày đầu tiên uống thuốc là \(9(mg)\)
Lượng thuốc kháng sinh đặc trị bệnh bạch hầu có trong cơ thể sau khi uống viên thuốc của ngày thứ \(2\) là \(159(mg)\)
Lượng thuốc kháng sinh đặc trị bệnh bạch hầu có trong cơ thể sau khi uống viên thuốc của ngày thứ \(4\) là \(170(mg)\)
Ước tính lượng thuốc kháng sinh đặc trị bệnh bạch hầu trong cơ thể nếu bệnh nhân sử dụng thuốc trong một thời gian 30 ngày là \(159,57mg\)
Câu 14:
Cho \(x,y\) là các số thực thỏa mãn \(f(x,y)={{\log }_{4}}\left( x+y \right)+{{\log }_{4}}\left( x-y \right)\ge 1\,\,(*)\).
Các khẳng định sau đúng hay sai?
Điều kiện xác định của hàm số \(f(x,y)\) là \(\left\{ \begin{align} & x+y>0 \\ & x-y>0 \\ \end{align} \right.\)
Với cặp số \(x,y\) thỏa mãn điều kiện xác định của hàm số \(f(x,y)\), ta có: \(f(x,y)={{x}^{2}}-{{y}^{2}}\)
Cặp số \(\left\{ \begin{align} & x=8 \\ & y=16 \\ \end{align} \right.\) thỏa mãn \(f(x,y)={{\log }_{4}}\left( x+y \right)+{{\log }_{4}}\left( x-y \right)\ge 1\)
Với \(P=2x-y\) thì \({{P}_{\min }}=2\sqrt{3}\)
Câu 15:
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\), \(SA\,\bot \,\left( ABCD \right)\), biết \(SC=a\sqrt{3}\). Gọi M, N, P, Q lần lượt là trung điểm của \(SB\), \(SD\), \(CD\), \(BC\). Các mệnh đề sau đúng hay sai?
Thể tích của khối chóp \(S.ABCD\) bằng \(\frac{1}{3}SA.{{S}_{ABCD}}\)
Thể tích của khối chóp \(S.ABC\) bằng thể tích của khối chóp \(S.ACD\)
Thể tích của khối chóp \(S.ABCD\) bằng \({{a}^{3}}\)
Thể tích của khối chóp \(A.MNPQ\) bằng \(\frac{{{a}^{3}}}{8}\)
Câu 16:
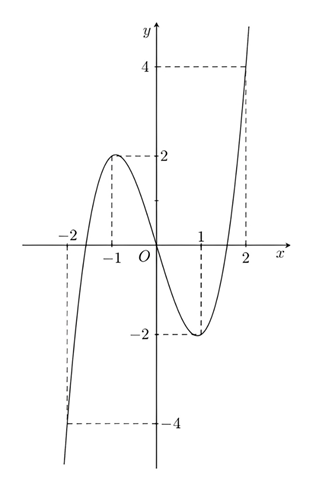
Cho hàm số \(y=f\left( x \right)\) xác định và liên tục trên \(\mathbb{R}\) có đồ thị như hình vẽ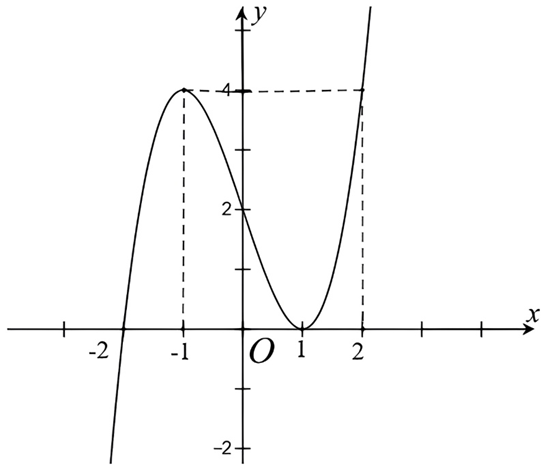
Các mệnh đề sau đây đúng hay sai?
Hàm số nghịch biến trên khoảng \(\left( -1;1 \right)\)
Hàm số có \({f}'\left( x \right)>0\) \(\forall x\in \left( -\infty ;-1 \right)\cup \left( 1;+\infty \right)\)
Hàm số \(g\left( x \right)=f\left( x \right)+1\) nghịch biến trên khoàng \(\left( 0;2 \right)\)
Hàm số \(y=f\left( \left| x \right| \right)\) đồng biến trên \(\left( -1;0 \right)\) và \(\left( 1;+\infty \right)\)