Đề thi thử Tốt nghiệp THPT năm 2025 môn Toán Sở GD&ĐT Thừa Thiên Huế - Đề 4
22 câu hỏi 60 phút
Tính tích phân \(I=\int_{-1}^{0}{\left( 2x+1 \right)}dx\)
\(I=0\)
\(I=1\)
\(I=2\)
\(I=-\frac{1}{2}\)
\(I=\mathop{\int }_{-1}^{0}\left( 2x+1 \right)dx=\left. \left( {{x}^{2}}+x \right) \right|_{-1}^{0}=0-0=0\).
Danh sách câu hỏi:
\(I=\mathop{\int }_{-1}^{0}\left( 2x+1 \right)dx=\left. \left( {{x}^{2}}+x \right) \right|_{-1}^{0}=0-0=0\).
Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y=f\left( x \right)\), trục hoành và hai đường thẳng \(x=a,x=b\) được tính bởi công thức:
\(S=\mathop{\int }_{a}^{b}\left| f\left( x \right) \right|\text{d}x\).
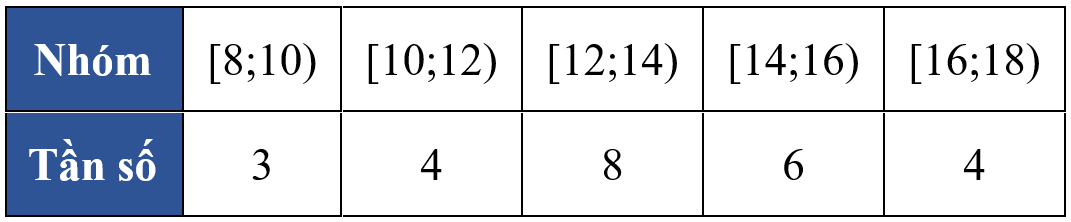
Tổng tần số: \(N=25\), khi đó số trung vị là số hạng: \({{x}_{13}}\in \left[ 12;14 \right)\).
Véctơ pháp tuyến của \(\left( P \right)\) là \({{\vec{n}}_{2}}\left( 2;3;1 \right)\).
Tiệm cận ngang \(\underset{x\to +\infty }{\mathop{\text{lim}}}\,y=\underset{x\to -\infty }{\mathop{\text{lim}}}\,y=\frac{4}{1}=4\).
Câu 8:
Cho hai đường thẳng phân biệt \(a, b\) và mặt phẳng \(\left( P \right)\). Chọn khẳng định đúng?
Câu 13:
Cho hàm số \(y=-{{x}^{3}}-3{{x}^{2}}-9x+3\) có đạo hàm trên \(\mathbb{R}\)
Hàm số có ba điểm cực trị
Hàm số nghịch biến trên tập xác định của nó
\(\underset{x\in \left( -4;4 \right]}{\mathop{\text{Min}}}\,f\left( x \right)=f\left( 4 \right)\)
Đồ thị hàm số \(y=-{{x}^{3}}-3{{x}^{2}}-9x+3\) cắt trục hoành tại 1 điểm duy nhất
Câu 14:
Sau khi xuất phát, ô tô di chuyển với tốc độ
\(v\left( t \right)=2,01t-0,025{{t}^{2}}\left( 0\le t\le 10 \right)\).
Trong đó \(v\left( t \right)\) tính theo \(\text{m}/\text{s}\), thời gian \(t\) tính theo \(s\) với \(t=0\) là thời điểm xe xuất phát
Quãng đường xe di chuyển được tính theo công thức là:
\(s\left( t \right)=2,01-0,05t\left( 0\le t\le 10 \right)\)
Quãng đường xe di chuyển được trong \(3\left( s \right)\) kể từ khi bắt đầu là \(8,82\left( \text{m} \right)\)
Quãng đường xe di chuyển được trong giây thứ 3 xấp xỉ 4,867(m)
Trong khoảng thời gian không quá 10 s đầu, khi vận tốc đạt giá trị lớn nhất thì gia tốc của xe là \(1,51\text{ }\!\!~\!\!\text{ m}/{{\text{s}}^{2}}\)
Câu 15:
Một công ty thiết bị Giáo Dục đấu thầu 2 dự án. Khả năng thắng thầu của dự án 1 là \(50\text{ }\!\!%\!\!\text{ }\) và dự án 2 là \(60\text{ }\!\!%\!\!\text{ }\). Khả năng thắng thầu cả 2 dự án là \(30\text{ }\!\!%\!\!\text{ }\). Gọi \(\text{A},\text{B}\) lần lượt là biến cố thắng thầu dự án 1 và dự án 2
A và B là hai biến độc lập
Xác suất công ty thắng thầu đúng 1 dự án là \(50\text{ }\!\!%\!\!\text{ }\)
Biết công ty thắng thầu dự án 1, xác suất công ty thắng thầu dự án 2 là \(60\text{ }\!\!%\!\!\text{ }\)
Biết công ty không thắng thầu dự án 1, xác suất công ty thắng thầu dự án 2 là \(60\text{ }\!\!%\!\!\text{ }\)
Câu 16:
Cho các điểm \(A\left( 1;-2;0 \right)\); \(B\left( 2;-1;1 \right)\); \(C\left( 1;1;2 \right)\)
Phương trình mặt phẳng \(\left( ABC \right)\) là
\(x+2y-3z-3=0\)
Phương trình mặt phẳng \(\left( \alpha \right)\) qua \(A\) và vuông góc với \(BC\) là:
\(x-2y-z-5=0\)
Phương trình mặt phẳng trung trực \(\left( \beta \right)\) của đoạn \(AC\) là:
\(6y+4z-1=0\)
Phương trình mặt phẳng \(\left( \gamma \right)\) chứa trục \(Ox\) và điểm \(C\) là:
\(2y+z=0\)