Trắc nghiệm Hai mặt phẳng vuông góc Toán Lớp 11
-
Câu 1:
Cho hình chóp tam giác đều S. ABC có độ dài cạnh đáy bằng a. Độ dài cạnh bên của hình chóp bằng bao nhiêu để góc giữa cạnh bên và mặt đáy bằng 600 ?
A. \(\frac{{2a}}{{\sqrt 3 }}.\)
B. \(\frac{{a}}{{\sqrt 3 }}.\)
C. \(\frac{{a}}{{\sqrt 2}}.\)
D. \(\frac{{2a}}{{\sqrt 2 }}.\)
-
Câu 2:
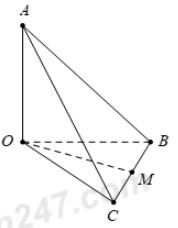
Cho tứ diện OABC có OA,OB,OC đôi một vuông góc với nhau và OA=OB=OC. Gọi M là trung điểm của BC (tham khảo hình vẽ bên). Góc giữa hai đường thẳng OM và AB bằng
A. 550
B. 600
C. 650
D. 700
-
Câu 3:
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, tâm của đáy là O. Gọi M và N lần lượt là trung điểm của SA và BC. Biết rằng góc giữa MN và (ABCD) bằng 60o, cosin góc giữa MN và mặt phẳng (SBD) bằng :
A. \(\frac{\sqrt{3}}{4}\)
B. \(\frac{2}{5}\)
C. \(\frac{\sqrt{5}}{5}\)
D. \(\frac{\sqrt{10}}{5}\)
-
Câu 4:
Cho hình lăng trụ đứng \(ABC.ABC\) có đáy là tam giác cân với \(AB=AC=a,\) góc \(\widehat{ABC}={{120}^{0}},\) cạnh bên BB’ = a. Gọi I là trung điểm của CC’. Tính cosin của góc giữa hai mặt phẳng (ABC) và (AB’I)?
A. cosα = \(\sqrt{\frac{3}{5}}\)
B. cosα=\(\sqrt{\frac{3}{10}}\)
C. cosα= \(\sqrt{\frac{7}{10}}\)
D. cosα = \(\sqrt{\frac{1}{2}}\)
-
Câu 5:
Cho hình lập phương ABCD. A’B’C’D’ có cạnh bằng a. Tính số đo góc giữa (BA’C) và (DA’C)
A. \({{30}^{0}}\)
B. \({{120}^{0}}\)
C. \({{60}^{0}}\)
D. \({{90}^{0}}\)
-
Câu 6:
Cho hình chóp tam giác S.ABC có đáy là tam giác đều cạnh 2a, có SA vuông góc với (ABC), tam giác SBC cân tại S. Để thể tích của khối chóp S.ABC là \(\frac{{{a}^{3}}\sqrt{3}}{2}\) thì góc giữa hai mặt phẳng (SBC) và (ABC) là:
A. \({{60}^{0}}\)
B. \({{30}^{0}}\)
C. \({{45}^{0}}\)
D. Đáp án khác.
-
Câu 7:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Mặt phẳng (SAB) vuông góc với đáy (ABCD). Gọi H là trung điểm của AB, \(SH=HC,SA=AB\). Gọi \(\alpha \) là góc giữa đường thẳng SC và mặt phẳng (ABCD). Giá trị của \(\tan \alpha \) là:
A. \(\frac{1}{\sqrt{2}}\)
B. \(\frac{2}{\sqrt{3}}\)
C. \(\frac{1}{\sqrt{3}}\)
D. \(\sqrt{2}\)
-
Câu 8:
Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Biết thể tích của hình chóp S.ABCD là \(\frac{{{a}^{3}}\sqrt{15}}{6}\). Góc giữa đường thẳng SC và mặt phẳng đáy (ABCD) là:
A. 300
B. 45o
C. 60o
D. 120o
-
Câu 9:
Cho hình chóp S.ABCD đáy ABCD là hình vuông cạnh a, \(\left( SAB \right)\bot \left( ABCD \right)\). H là trung điểm của AB, \(SH=HC,SA=AB\). Gọi a là góc giữa đường thẳng SC và mặt phẳng (ABCD). Giá trị của \(\tan \alpha \) là:
A. \(\frac{1}{\sqrt{2}}\)
B. \(\frac{2}{\sqrt{3}}\)
C. \(\frac{1}{\sqrt{3}}\)
D. \(\sqrt{2}\)
-
Câu 10:
Cho hình chóp S.ABC có đường cao SA bằng 2a, tam giác ABC vuông ở C có \(AB=2a,\) \(\widehat{CAB}={{30}^{0}}\). Gọi H là hình chiếu vuông của A trên SC. Tính theo a thể tích của khối chóp H.ABC. Tính cô-sin của góc giữa hai mặt phẳng \(\left( SAB \right),\,\,\left( SBC \right).\)
A. \(\frac{\sqrt{7}}{7}\)
B. \(\frac{\sqrt{7}}{14}\)
C. \(\frac{3\sqrt{7}}{14}\)
D. \(\frac{\sqrt{7}}{9}\)
-
Câu 11:
Cho khối chóp tứ giác đều \(S.ABCD\) có tất cả các cạnh bằng a. Khi đó côsin góc giữa mặt bên và mặt đáy là:
A. \({{30}^{O}}\)
B. \(\sqrt{3}\)
C. \({{60}^{O}}\)
D. \(\frac{1}{\sqrt{3}}\)
-
Câu 12:
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và S, SA vuông góc với mặt phẳng đáy. Tính cô-sin góc giữa 2 đường thẳng SD và BC biết \(AD=D C=a, A B=2 a, S A=\frac{2 \sqrt{3} a}{3}\)
A. \(\frac{1}{\sqrt{42}}\)
B. \(\frac{2}{\sqrt{42}}\)
C. \(\frac{3}{\sqrt{42}}\)
D. \(\frac{4}{\sqrt{42}}\)
-
Câu 13:
Cho hình lăng trụ tam giác đều \(A B C . A^{\prime} B^{\prime} C^{\prime} \text { có } A B=a\,và\,A A^{\prime}=\sqrt{2} a\). Góc giữa hai đường thẳng AB' và BC' bằng
A. \(30^{\circ} .\)
B. \(60^{\circ} .\)
C. \(90^{\circ} .\)
D. \(45^{\circ} .\)
-
Câu 14:
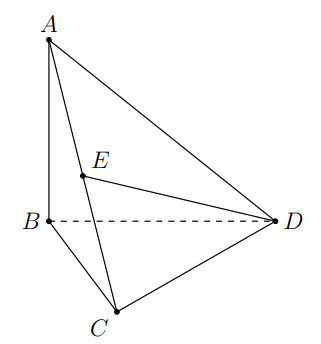
Cho tứ diện đều ABCD. Gọi M là trung điểm cạnh BC (tham khảo hình vẽ bên). Giá trị cô-sin của góc giữa hai đường thẳng AB và DM bằng
A. \(\begin{array}{llll} \frac{\sqrt{3}}{6} \end{array}\)
B. \(\frac{\sqrt{3}}{3} \)
C. \( \frac{\sqrt{3}}{2}\)
D. \( \frac{1}{2} .\)
-
Câu 15:
Cho hình chóp tứ giác đều S.ABCD đáy ABCD là hình vuông, E là điểm đối xứng với D qua trung điểm SA. Gọi M, N lần lượt là trung điểm của AE và BC. Góc giữa hai đường thẳng MN và BD bằng:
A. \(90^{\circ} .\)
B. \(60^{\circ} .\)
C. \(30^{\circ} .\)
D. \(45^{\circ} .\)
-
Câu 16:
Cho hình lập phương \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}\). Góc giữa hai đường thẳng AC và A'D bằng
A. \(45^{\circ} .\)
B. \(90^{\circ} .\)
C. \(30^{\circ} .\)
D. \(60^{\circ} .\)
-
Câu 17:
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh BC và AD. Biết \(A B=C D=2 a, M N=a \sqrt{3}\). Tính góc giữa hai đường thẳng AB và CD
A. \(90^{\circ} .\)
B. \(45^{\circ} .\)
C. \(30^{\circ} .\)
D. \(60^{\circ} .\)
-
Câu 18:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, cạnh bên SA vuông góc với đáy, SA = a. Gọi M là trung điểm của SB. Góc giữa AM và BD bằng
A. \(45^{\circ}\)
B. \(30^{\circ}\)
C. \(60^{\circ}\)
D. \(90^{\circ}\)
-
Câu 19:
Tứ diện đều ABCD cạnh a, M là trung điểm của cạnh CD. Cô-sin của góc giữa AM và BD là
A. \(\frac{\sqrt{3}}{6}\)
B. \(\frac{\sqrt{2}}{6}\)
C. \(\frac{\sqrt{3}}{3}\)
D. \(\frac{\sqrt{2}}{3}\)
-
Câu 20:
Cho hình chóp S.ABC có tất cả các cạnh đều bằng a. Gọi I, J lần lượt là trung điểm của SA, BC. Tính số đo của góc hợp bởi IJ và SB.
A. \(45^{\circ} .\)
B. \(30^{\circ} .\)
C. \(60^{\circ} .\)
D. \(90^{\circ} .\)
-
Câu 21:
Cho hình lập phương \(A B C D . A^{\prime} B^{\prime} C^{\prime} D^{\prime}\) cạnh a.Gọi M, N, P lần lượt là trung điểm các cạnh A B, B C, C'D'. Xác định góc giữa hai đường thẳng MN và AP.
A. \(60^{\circ} .\)
B. \(90^{\circ} .\)
C. \(30^{\circ} .\)
D. \(45^{\circ} .\)
-
Câu 22:
Cho hình chóp S.ABC có SA = SB = SC = AB = AC = 1, \(B C=\sqrt{2}\). Tính góc giữa hai đường thẳng AB, SC
A. \(\begin{array}{llll} 45^{\circ} . \end{array}\)
B. \(120^{\circ} . \)
C. \(30^{\circ} . \)
D. \(60^{\circ} .\)
-
Câu 23:
Cho hình lập phương \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}\) . Góc giữa \(A^{\prime} C^{\prime} \text { và } D^{\prime} C^{\prime}\) là
A. \(\begin{array}{llll} 120^{\circ} \end{array}\)
B. \(45^{\circ} . \)
C. \( 60^{\circ} . \)
D. \(90^{\circ} .\)
-
Câu 24:
Cho tứ diện ABCD có AB vuông góc với mặt phẳng (BCD). Biết tam giác BCD vuông tại C và \(A B=\frac{a \sqrt{6}}{2}, A C=a \sqrt{2}, C D=a\). Gọi E là trung điểm của AD. Góc giữa hai đường thẳng AB và CE bằng
A. \(\begin{array}{ll} 45^{\circ} . \end{array}\)
B. \(60^{\circ} .\)
C. \(30^{\circ} . \)
D. \(90^{\circ} .\)
-
Câu 25:
Cho tứ diện đều ABCD có M là trung điểm của cạnh CD , \(\varphi\) là góc giữa hai đường thẳng AM và BC. Giá trị \(\cos \varphi\) bằng
A. \(\begin{array}{ll} \frac{\sqrt{3}}{6} \end{array}\)
B. \( \frac{\sqrt{3}}{4} .\)
C. \(\frac{\sqrt{2}}{3} . \)
D. \(\frac{\sqrt{2}}{6} .\)
-
Câu 26:
Cho hình lăng trụ đứng tam giác ABC:A0B0C0 có đáy ABC là tam giác cân, \(A B=A C=a, \widehat{B A C}=120^{\circ}\)cạnh bên \(A A^{\prime}=a \sqrt{2}\). Tính góc giữa hai đường thẳng AB' và BC.
A. \(\begin{array}{llll} 90^{\circ} \end{array}\)
B. \(30^{\circ} . \)
C. \( 45^{\circ} . \)
D. \( 60^{\circ} .\)
-
Câu 27:
Cho tứ diện ABCD có AB vuông góc với mặt phẳng (BCD). Biết tam giác BCD vuông tại C và \(A B=\frac{a \sqrt{6}}{2}, A C=a \sqrt{2}, C D=a\). Gọi E là trung điểm của AD. Góc giữa hai đường thfẳng AB và CE bằng:
A. \(60^{\circ} \)
B. \(45^{\circ}\)
C. \(30^{\circ}\)
D. \(90^{\circ}\)
-
Câu 28:
Cho tứ diện ABCD có AB vuông góc với mặt phẳng (B C D). Biết tam giác BCD vuông tại C và \(A B=\frac{a \sqrt{6}}{2}, A C=a \sqrt{2}, C D=a\). Gọi E là trung điểm của AC (tham khảo hình vẽ bên). Góc giữa hai đường thẳng A B và DE bằng
A. \(\begin{array}{llll} 45^{\circ} \end{array}\)
B. \(60^{\circ} .\)
C. \(30^{\circ}\)
D. \(90^{\circ} .\)
-
Câu 29:
Cho tứ diện đều ABCD cạnh a= 12, gọi (P) là mặt phẳng qua B và vuông góc với AD. Thiết diện của (P) và hình chóp có diện tích bằng
A. \(\begin{array}{lllll} 36 \sqrt{2} \end{array}\)
B. \(40\)
C. \( 36 \sqrt{3}\)
D. \(36\)
-
Câu 30:
Cho hình chóp tam giác đều S.ABC với SA= 2AB . Góc giữa (SAB) và (ABC) bằng \(\alpha\) . Chọn khẳng định đúng trong các khẳng định sau?
A. \(alpha=60^{\circ}\)
B. \(\cos \alpha=\frac{1}{3 \sqrt{5}}\)
C. \(\cos \alpha=\frac{1}{4 \sqrt{5}}\)
D. \(\cos \alpha=\frac{1}{2 \sqrt{5}}\)
-
Câu 31:
Cho hình chóp S ABCD . có đáy ABCD là hình vuông tâm O . Biết \(S O \perp(A B C D)\), \(S O=a \sqrt{3}\) và đường tròn ngoại tiếp ABCD có bán kính bằng a . Gọi \(\alpha\) là góc hợp bởi mặt bên (SCD) với đáy. Khi đó \(\tan \alpha=?\)
A. \(\frac{\sqrt{3}}{2}\)
B. \(\frac{\sqrt{3}}{\sqrt{2}}\)
C. \(\frac{\sqrt{6}}{6}\)
D. \(\sqrt{6}\)
-
Câu 32:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông và \(S A \perp(A B C D)\), gọi O là tâm hình vuông ABCD . Khẳng định nào sau đây sai?
A. Góc giữa hai mặt phẳng \((S B C) \text { và }(A B C D) \text { là góc } \widehat{A B S}\)
B. Góc giữa hai mặt phẳng \((S B D) \text { và }(A B C D) \text { là góc } \widehat{S O A}\)
C. Góc giữa hai mặt phẳng (SAD) và (ABCD) là góc \(\widehat{S D A}\)
D. \((S A C) \perp(S B D)\)
-
Câu 33:
Cho hình chóp S.ABC có \(S A \perp(A B C)\) và AB BC , gọi I là trung điểm BC . Góc giữa hai mặt phẳng \((S B C) \text { và }(A B C)\) là góc nào sau đây?
A. Góc SBA.
B. Góc SCA .
C. Góc SCB .
D. Góc SIA.
-
Câu 34:
Cho hình chóp S.ABC có \(S A \perp(A B C)\) và đáy ABC vuông ở A . Khẳng định nào sau đây sai ?
A. \(\begin{array}{l} (S A B) \perp(A B C) \end{array}\)
B. \((S A B) \perp(S A C)\)
C. Vẽ \(A H \perp B C, H \in B C \Rightarrow\) góc AHS là góc giữa hai mặt phẳng (SBC) và (ABC) .
D. Góc giữa hai mặt phẳng (SBC) và (AC) là góc \(\widehat{S C B}\)
-
Câu 35:
Cho hình chóp tứ giác đều S.ABCD, có đáy ABCD là hình vuông tâm O . Các cạnh bên và các cạnh đáy đều bằng a . Gọi M là trung điểm SC . Góc giữa hai mặt phẳng (MBD) và (ABCD) bằng:
A. \(90^{0} .\)
B. \(60^{0} .\)
C. \(30^{0} .\)
D. \(45^{0} .\)
-
Câu 36:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và có \(S A=S B=S C=a\) . Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng?
A. \(30^{\circ}\)
B. \(90^{\circ}\)
C. \(60^{\circ}\)
D. \(45^{\circ}\)
-
Câu 37:
Cho hình chóp S ABC . có hai mặt bên (SAB) và (SAC) vuông góc với mặt phẳng (ABC) , tam giác ABC vuông cân ở A và có đường cao \(A H(H \in B C)\) . Gọi O là hình chiếu vuông góc của A lên (S B C) . Khẳng định nào sau đây sai ?
A. \(S C \perp(A B C)\)
B. \(O \in S H\)
C. \((S A H) \perp(S B C)\)
D. \(((S B C),(A B C))=\widehat{S B A}\)
-
Câu 38:
Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng a . Tính cosin của góc giữa một mặt bên và một mặt đáy
A. \(\frac{1}{2}\)
B. \(\frac{1}{3}\)
C. \(\frac{1}{\sqrt{3}}\)
D. \(\frac{1}{\sqrt{2}}\)
-
Câu 39:
Cho tứ diện đều ABCD . Góc giữa (ABC) và (ABD) bằng \(\alpha\) . Chọn khẳng định đúng trong các khẳng định sau?
A. \(\cos \alpha=\frac{1}{3}\)
B. \(\cos \alpha=\frac{1}{4}\)
C. \(\alpha=60^{\circ}\)
D. \(\cos \alpha=\frac{1}{5}\)
-
Câu 40:
Cho hình chóp tứ giác S.ABCD, có đáy ABCD là hình thoi tâm I cạnh bằng A và góc \(\hat{A}=60^{\circ}\) , cạnh \(S C=\frac{a \sqrt{6}}{2}\) và SC vuông góc với mặt phẳng \((A B C D)\) . Trong tam giác SAC kẻ \(I K \perp S A\) tại K . Tính số đo góc \(\widehat{\mathrm{BKD}}\)
A. \(60^{\circ}\)
B. \(45^{\circ}\)
C. \(90^{\circ}\)
D. \(30^{\circ}\)
-
Câu 41:
Cho tứ diện ABCD có \(A C=A D \text { và } B C=B D\) . Gọi I là trung điểm của CD . Khẳng định nào sau đây sai?
A. Góc giữa hai mặt phẳng (ABC) và (ABD) là \(\widehat{C B D}\).
B. Góc giữa hai mặt phẳng (ACD) và (BCD) là \(\widehat{A I B}\)
C. \(\begin{array}{l} (B C D) \perp(A I B) \end{array}\)
D. \((A C D) \perp(A I B)\)
-
Câu 42:
Trong các mệnh đề sau, mệnh đề nào sai?
A. Hình lăng trụ tam giác có hai mặt bên là hình chữ nhật là hình lăng trụ đứng.
B. Hình chóp có đáy là đa giác đều và có các cạnh bên bằng nhau là hình chóp đều.
C. Hình lăng trụ đứng có đáy là đa giác đều là hình lăng trụ đều.
D. Hình lăng trụ có đáy là đa giác đều là hình lăng trụ đều.
-
Câu 43:
Mệnh đề nào sau đây là đúng?
A. Hai mặt phẳng vuông góc với nhau thì mọi đường thẳng nằm trong mặt phẳng này sẽ vuông góc với mặt phẳng kia.
B. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì vuông góc với nhau.
C. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
D. Hai mặt phẳng vuông góc với nhau thì mọi đường thẳng nằm trong mặt phẳng này và vuông góc với giao tuyến của hai mặt phẳng sẽ vuông góc với mặt phẳng kia
-
Câu 44:
Cho các mệnh đề sau với \((\alpha) \text { và }(\beta)\) là hai mặt phẳng vuông góc với nhau với giao tuyến \(m=(\alpha) \cap(\beta) \) và a, b, c, d là các đường thẳng. Các mệnh đề sau, mệnh đề nào đúng?
A. Nếu \(b \perp m \text { thì } b \subset(\alpha) \text { hoặc } b \subset(\beta)\)
B. Nếu \(b \perp m \text { thì } d \perp(\alpha)\)
C. Nếu \(a \subset(\alpha) \text { và } a \perp m \text { thì } a \perp(\beta)\)
D. Nếu \(\mathrm{c}/ / \mathrm{m} \text { thì } \mathrm{c} / /(\alpha) \text { hoăc } \mathrm{c}/ /(\beta)\)
-
Câu 45:
Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai mặt phẳng cùng song song với một mặt phẳng thứ ba thì song song với nhau.
B. Qua một đường thẳng cho trước có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.
C. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với hai mặt phẳng cắt nhau cho trước.
D. Hai mặt phẳng cùng vuông góc với một mặt phẳng thứ ba thì vuông góc với nhau
-
Câu 46:
Cho hai mặt phẳng (P) và (Q) , a là một đường thẳng nằm trên (P). Mệnh đề nào sau đây sai?
A. Nếu \(a / / b \text { với } b=(P) \cap(O) \text { thì a } / /(O)\)
B. Nếu \((P) \perp(Q) \text { thì } a \perp(Q)\)
C. \(Nếu \,a \text { cắt }(Q) \text { thì }(P) \text { cắt }(Q)\)
D. Nếu \((P) / /(Q) \text { thì } a / /(Q)\)
-
Câu 47:
Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai mặt phẳng cùng vuông góc với một mặt phẳng thứ ba thì vuông góc với nhau.
B. Qua một đường thẳng cho trước có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.
C. Các mặt phẳng cùng đi qua một điểm và vuông góc với một mặt phẳng cho trước thì luôn đi qua một đường thẳng cố định.
D. Hai mặt phẳng cùng vuông góc với mặt phẳng thứ ba thì vuông góc với nhau.
-
Câu 48:
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Cắt hình lập phương bởi mặt phẳng trung trực của AC'. Diện tích thiết diện là
A. \(S = \frac{{{a^2}\sqrt 3 }}{2}.\)
B. \(S = {a^2}.\)
C. \(S = \frac{{{a^2}\sqrt 3 }}{4}.\)
D. \(S={a^2}\frac{{3\sqrt 3 }}{4}\)
-
Câu 49:
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Cắt hình lập phương bởi mặt phẳng trung trực của AC'. Thiết diện là hình gì?
A. Hình vuông.
B. Lục giác đều.
C. Ngũ giác đều.
D. Tam giác đều.
-
Câu 50:
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại A, với AB = c, AC = b, cạnh bên AA' = h. Mặt phẳng (P) đi qua A' và vuông góc với B'C.Thiết diện của lăng trụ cắt bởi mặt phẳng (P) có hình:
.png)
A. h1 và h2
B. h2 và h3
C. h2
D. h1
