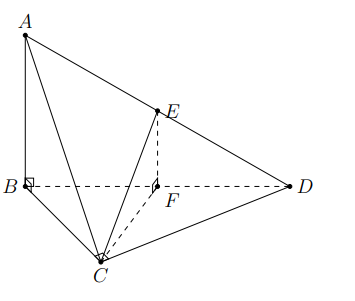
Cho tứ diện ABCD có AB vuông góc với mặt phẳng (BCD). Biết tam giác BCD vuông tại C và \(A B=\frac{a \sqrt{6}}{2}, A C=a \sqrt{2}, C D=a\). Gọi E là trung điểm của AD. Góc giữa hai đường thfẳng AB và CE bằng:
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai
\(\begin{aligned} &\text { Gọi } F \text { là trung điểm của } B D \text { , suy ra } E F \text { // } A B \text { nên }(A B, C E)=(E F, C E) \end{aligned}\)
\(\text { Do } A B \perp(B C D) \text { nên } E F \perp(B C D), \text { suy ra } \triangle E F C\) vuông tại F.
\(\begin{array}{l} \text { Mặt khác }\left\{\begin{array}{l} C D \perp B C \\ C D \perp A B \end{array} \Rightarrow C D \perp A C\right. \\ \text { Ta có } E F=\frac{1}{2} A B=\frac{a \sqrt{6}}{4}, A D=\sqrt{A C^{2}+C D^{2}}=a \sqrt{3} . \end{array}\)
tam giác ACD vuông tại C và có E là trung điểm của AD nên \(C E=\frac{1}{2} A D=\frac{a \sqrt{3}}{2}\)
\(\begin{array}{l} C E=\frac{1}{2} A D=\frac{a \sqrt{3}}{2} \\ \cos \widehat{C E F}=\frac{E F}{E C}=\frac{\sqrt{2}}{2} \Rightarrow \widehat{C E F}=45^{\circ} \\ \text { Vậy }(A B, C E)=(E F, C E)=\widehat{C E F}=45^{\circ} . \end{array}\)
Câu hỏi liên quan
-
Cho hình chóp S.ABC có hai mặt bên (SBC) và (SAC) vuông góc với đáy (ABC). Khẳng định nào sau đây sai?
-
Cho hình chóp tứ giác S.ABCD, có đáy ABCD là hình thoi tâm I cạnh bằng A và góc \(\hat{A}=60^{\circ}\) , cạnh \(S C=\frac{a \sqrt{6}}{2}\) và SC vuông góc với mặt phẳng \((A B C D)\) . Trong tam giác SAC kẻ \(I K \perp S A\) tại K . Tính số đo góc \(\widehat{\mathrm{BKD}}\)
-
Hình hộp ABCD.A'B'C'D' trở thành hình lăng trụ tứ giác đều khi phải thêm các điều kiện nào sau đây?
-
Cho tam giác đều ABC cạnh a. Gọi \({d_B},{d_C}\) lần lượt là đường thẳng đi qua B, C và vuông góc với (ABC). (P) là mặt phẳng qua A và hợp với (ABC) góc 60o. (P) cắt \({d_B},{d_C}\) lần lượt tại D và E. Biết \(AD = a\frac{{\sqrt 6 }}{2},AE = a\sqrt 3 .\) Đặt \(\widehat {DAE} = \varphi \). Chọn khẳng định đúng trong các khẳng định sau?
-
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khẳng định nào sau đây sai?
-
Cho hình chóp tứ giác đều S.ABCD, có đáy ABCD là hình vuông tâm O . Các cạnh bên và các cạnh đáy đều bằng a . Gọi M là trung điểm SC . Góc giữa hai mặt phẳng (MBD) và (ABCD) bằng:
-
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, cạnh bên SA vuông góc với đáy, SA = a. Gọi M là trung điểm của SB. Góc giữa AM và BD bằng
-
Cho hình chóp tứ giác đều S.ABCD có SA = SB. Góc giữa (SAB) và (SAD) bằng \(\alpha\). Chọn khẳng định đúng trong các khẳng định sau?
-
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và có \(S A=S B=S C=a\) . Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng?
-
Cho hai mặt phẳng (P) và (Q) , a là một đường thẳng nằm trên (P). Mệnh đề nào sau đây sai?
-
Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Biết thể tích của hình chóp S.ABCD là \(\frac{{{a}^{3}}\sqrt{15}}{6}\). Góc giữa đường thẳng SC và mặt phẳng đáy (ABCD) là:
-
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA ⊥ (ABC) và SA = a/2.
M là trung điểm của BC. Khi đó góc giữa hai mặt phẳng (SAM) và (SBC) bằng:
-
Cho hình lăng trụ tứ giác đều ABCD.A'B'C'D' có ACC'A' là hình vuông, cạnh bằng a. Cạnh đáy của hình lăng trụ bằng:
-
Mệnh đề nào sau đây là đúng?
-
Trong các mệnh đề sau, mệnh đề nào đúng?
-
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và góc giữa cạnh bên với mặt phẳng đáy bằng ∝
Tan của góc giữa mặt bên và mặt đáy bằng:
-
Cho hình lăng trụ đứng ABC.A'B'C' có AB = AA' = a, BC = 2a, \(CA = a\sqrt 5 \). Khẳng định nào sau đây sai?
-
Cho hình chóp S.ABCD có đáy là hình thoi tâm O cạnh a và có góc \(\widehat {BAD} = {60^0}\). Đường thẳng SO vuông góc với mặt phẳng đáy (ABCD) và \(SO = \frac{{3a}}{4}\). Gọi E là trung điểm BC và F là trung điểm BE. Góc giữa hai mặt phẳng (SOF) và (SBC) là
-
Cho hình chóp S.ABCD có ABCD là hình chữ nhật. SA vuông góc với (ABCD), AH và AK lần lượt là đường cao của tam giác SAB và SAD.
Hai mặt phẳng (SAC) và (AHK) vuông góc vì:
.png)
-
Cho tứ diện ABCD có AC = AD và BC = BD. Gọi I là trung điểm của CD. Khẳng định nào sau đây sai?
