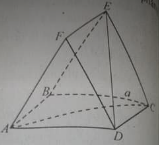
Cho hình chóp S.ABCD có hai mặt bên (SAB) và (SAC) vuông góc với mặt phẳng (ABC), tam giác ABC vuông cân ở A và có đường cao AH \(\left( {H \in BC} \right)\). Gọi O là hình chiếu vuông góc của A lên (SBC). Khẳng định nào sau đây sai ?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai.png)
Ta có \(\left. \begin{array}{l} \left( {SAB} \right) \bot \left( {ABC} \right)\\ \left( {SAC} \right) \bot \left( {ABC} \right)\\ \left( {SAB} \right) \cap \left( {SAC} \right) = SA \end{array} \right\} \Rightarrow SA \bot \left( {ABC} \right) \Rightarrow SA \bot BC\).
\(\left. \begin{array}{l} BC \bot AH\\ BC \bot SA \end{array} \right\} \Rightarrow BC \bot \left( {SAH} \right) \Rightarrow BC \bot SH\).
Mặt khác, \(AH \bot BC\) nên \(\left( {\left( {SBC} \right),\left( {ABC} \right)} \right) = \left( {SH,AH} \right) = \widehat {SHA}\).
Câu hỏi liên quan
-
Cho hình chóp tứ giác đều S.ABCD có SA = SB. Góc giữa (SAB) và (SAD) bằng \(\alpha\). Chọn khẳng định đúng trong các khẳng định sau?
-
Cho hình chóp S.ABCD có đáy ABCD là hình vuông và \(SA \bot \left( {ABCD} \right)\), gọi O là tâm hình vuông ABCD. Khẳng định nào sau đây sai?
-
Cho tứ diện ABCD có AB vuông góc với mặt phẳng (B C D). Biết tam giác BCD vuông tại C và \(A B=\frac{a \sqrt{6}}{2}, A C=a \sqrt{2}, C D=a\). Gọi E là trung điểm của AC (tham khảo hình vẽ bên). Góc giữa hai đường thẳng A B và DE bằng
-
Cho hai mặt phẳng (P) và (Q) , a là một đường thẳng nằm trên (P). Mệnh đề nào sau đây sai?
-
Cho hai hình vuông ABCD và ABEF cạnh a nằm trên hai mặt phẳng vuông góc. Đường thẳng DE vuông góc?
-
Cho tứ diện ABCD có: AB = AC = AD, góc BAC bằng góc BAD bằng 60o. Gọi M và N lần lượt là trung điểm của AB và CD.
Góc giữa hai mặt phẳng (ACD) và (BCD) là:
-
Chỉ ra mệnh đề đúng trong các mệnh đề sau:
-
Cho hình chóp S.ABC có SA = SB = SC = AB = AC = 1, \(B C=\sqrt{2}\). Tính góc giữa hai đường thẳng AB, SC
-
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân ở A. H là trung điểm BC. Khẳng định nào sau đây sai ?
-
Cho hình chóp S.ABCD, đáy ABCD là hình vuông, \(SA \bot (ABCD)\). Gọi \((\alpha)\) là mặt phẳng chứa AB và vuông góc với (SCD), \((\alpha)\) cắt chóp S.ABCD theo thiết diện là hình gì?
-
Cho hai tam giác ACD và BCD nằm trên hai mặt phẳng vuông góc với nhau và \(AC = AD = BC = BD = a;CD = 2x\). Với giá trị nào của x thì hai mặt phẳng (ABC) và (ABD) vuông góc.
-
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Cắt hình lập phương bởi mặt phẳng trung trực của AC'. Thiết diện là hình gì?
-
Cho hình chóp tam giác đều S. ABC có độ dài cạnh đáy bằng a. Độ dài cạnh bên của hình chóp bằng bao nhiêu để góc giữa cạnh bên và mặt đáy bằng 600 ?
-
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA ⊥ (ABC) và SA = a/2.
Góc giữa hai mặt phẳng (SAB) và (ABC) bằng:
-
Cho các mệnh đề sau với \((\alpha)\) và \((\beta)\) là hai mặt phẳng vuông góc với nhau với giao tuyến \(m = \left( \alpha \right) \cap \left( \beta \right)\) và a, b, c, d là các đường thẳng. Các mệnh đề sau, mệnh đề nào đúng?
-
Cho hình lăng trụ ABCD.A'B'C'D'. Hình chiếu vuông góc của A' lên (ABC) trùng với trực tâm H của tam giác ABC. Khẳng định nào sau đây không đúng?
-
Cho hình hộp chữ nhật ABCD.A'B'C'D'. Khẳng định nào sau đây không đúng?
-
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và đường cao SH bằng cạnh đáy. Tính số đo góc hợp bởi cạnh bên và mặt đáy.
-
Cho hình thoi ABCD có cạnh bằng a và \(\widehat A = 60^\circ \). Trên đường thẳng vuông góc với mặt phẳng (ABCD) tại O (O là tâm của ABCD), lấy điểm S sao cho tam giác SAC là tam giác đều. Khẳng định nào sau đây đúng?
-
Cho hình chóp cụt đều ABC.A'B'C' với đáy lớn ABC có cạnh bằng a. Đáy nhỏ A'B'C' có cạnh bằng \(\frac{a}{2}\), chiều cao \(OO' = \frac{a}{2}\). Khẳng định nào sau đây sai?
