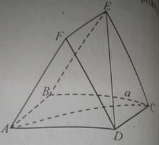
Cho hình chóp đều S.ABC có cạnh đáy bằng a, góc giữa một mặt bên và mặt đáy bằng 60^o. Tính độ dài đường cao SH.

Cho hình chóp tam giác đều S. ABC có độ dài cạnh đáy bằng a. Độ dài cạnh bên của hình chóp bằng bao nhiêu để góc giữa cạnh bên và mặt đáy bằng 60⁰ ?

Cho hình chóp tứ giác đều S.ABCD, có đáy ABCD là hình vuông tâm O. Các cạnh bên và các cạnh đáy đều bằng A. Gọi M là trung điểm SC. Góc giữa hai mặt phẳng (MBD) và (ABCD) bằng:

Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O. Biết \(SO \bot \left( {ABCD} \right),SO = a\sqrt 3 \) và đường tròn nội tiếp ABCD có bán kính bằng a. Tính góc hợp bởi mỗi mặt bên với đáy.

Cho hình lăng trụ tứ giác đều ABCD.A'B'C'D' có cạnh đáy bằng a, góc giữa hai mặt phẳng (ABCD) và (ABC') có số đo bằng 60^o. Cạnh bên của hình lăng trụ bằng:

Cho hình lập phương ABCD. A’B’C’D’ có cạnh bằng a. Tính số đo góc giữa (BA’C) và (DA’C)

Cho hình chóp S.ABCD có ABCD là hình chữ nhật. SA vuông góc với (ABCD), AH và AK lần lượt là đường cao của tam giác SAB và SAD.

Hai mặt phẳng (SAB) và (SBC) vuông góc vì.

Cho hình chóp S.ABC có SA = SB = SC = AB = AC = 1, \(B C=\sqrt{2}\). Tính góc giữa hai đường thẳng AB, SC

Trong các mệnh đề sau, mệnh đề nào sai?

Trong các mệnh đề sau, mệnh đề nào đúng?

Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và có SA = SB = SC = a. Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng

Cho tam giác ABC vuông tại A. Cạnh AB = a nằm trong mặt phẳng (P), cạnh \(AC = a\sqrt 2 \), AC tạo với (P) một góc 60^o. Chọn khẳng định đúng trong các khẳng định sau?

Cho hình chóp S.ABC có đường cao SA bằng 2a, tam giác ABC vuông ở C có \(AB=2a,\) \(\widehat{CAB}={{30}^{0}}\). Gọi H là hình chiếu vuông của A trên SC. Tính theo a thể tích của khối chóp H.ABC. Tính cô-sin của góc giữa hai mặt phẳng \(\left( SAB \right),\,\,\left( SBC \right).\)

Cho hình chóp S.ABC có \(S A \perp(A B C)\) và đáy ABC vuông ở A . Khẳng định nào sau đây sai ? 

Cho hình thoi ABCD có cạnh bằng a và \(\widehat A = 60^\circ \). Trên đường thẳng vuông góc với mặt phẳng (ABCD) tại O (O là tâm của ABCD), lấy điểm S sao cho tam giác SAC là tam giác đều. Khẳng định nào sau đây đúng?

Cho tam giác ABC và mặt phẳng (P). Biết góc giữa mặt phẳng (P) và mặt phẳng (ABC) là \(\varphi \). Hình chiếu của tam giác ABC trên mặt phẳng (P) là tam giác A'B'C'.  Tìm hệ thức liên hệ giữa diện tích tam giác ABC và diện tích tam giác A'B'C'.

Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và SA = SB = SC = a.

Góc giữa mặt bên hình chóp S.ABCD và mặt phẳng đáy có tang bằng:

Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA ⊥ (ABC) và SA = a/2.

Góc giữa hai mặt phẳng (SAB) và (ABC) bằng:

Trong các mệnh đề sau, mệnh đề nào đúng?

Cho hình chóp S.ABCD với ABCD là hình chữ nhật tâm O có \(AB = a,{\rm{ }}AD = 2a.{\rm{ }}SA\) vuông góc với đáy và SA = a. Gọi (P) là mặt phẳng qua SO và vuông góc với (SAD). Diện tích thiết diện của (P) và hình chóp S.ABCD bằng bao nhiêu?

Cho tứ diện đều ABCD. Góc giữa (ABC) và (ABD) bằng \(\alpha\). Chọn khẳng định đúng trong các khẳng định sau?