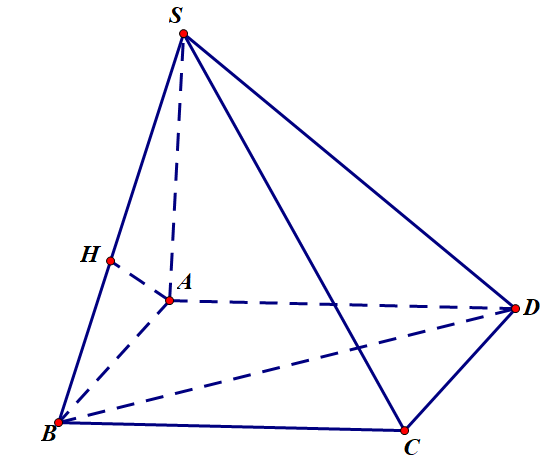
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, cạnh bên SA vuông góc với đáy, SA = a. Gọi M là trung điểm của SB. Góc giữa AM và BD bằng
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có
\(\begin{aligned} &\begin{aligned} & 2 \overrightarrow{A M} \cdot \overrightarrow{B D}=(\overrightarrow{A S}+\overrightarrow{A B}) \overrightarrow{B D}=\overrightarrow{A B} \cdot \overrightarrow{B D} \\ =& A B \cdot B D \cdot \cos 135^{\circ}=-\frac{a \cdot a \sqrt{2} \sqrt{2}}{2}=-a^{2} . \end{aligned}\\ &\text { Từ đó }\\ &\cos (\overrightarrow{A M} ; \overrightarrow{B D})=\frac{\overrightarrow{A M} \cdot \overrightarrow{B D}}{A M \cdot B D}=\frac{-\frac{a^{2}}{2}}{\frac{a \sqrt{2}}{2} \cdot a \sqrt{2}}\\ &=-\frac{1}{2} \Rightarrow(\overrightarrow{A M} ; \overrightarrow{B D})=120^{\circ} \end{aligned}\)
Vậy góc giữa AM và BD bằng \(60^{\circ}\)