Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và góc giữa cạnh bên với mặt phẳng đáy bằng ∝
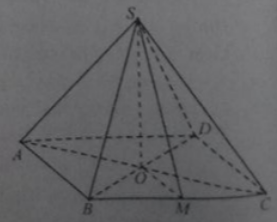
Tan của góc giữa mặt bên và mặt đáy bằng:
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiChân đường cao hình chóp đều S.ABCD trùng với tâm O của đáy ABCD. AO là hình chiếu của SA lên (ABCD.
\( \Rightarrow \widehat {SAO} = \alpha \)
Gọi M là trung điểm của BC, suy ra OM là hình chiếu của SM lên (ABCD) và \(MO\bot BC\)
\(\begin{array}{l}
\widehat {SMO} = \left( {\widehat {\left( {SBC} \right),\left( {ABCD} \right)}} \right)\\
AC = a\sqrt 2 ,AO = \frac{1}{2}AC = \frac{{a\sqrt 2 }}{2}\\
SO = OA.\tan \widehat {SAO} = \frac{{a\sqrt 2 }}{2}.\tan \alpha \\
OM = \frac{{AB}}{2} = \frac{a}{2},\tan \widehat {SMO} = \frac{{SO}}{{OM}} = \frac{{a\sqrt 2 }}{2}\tan \alpha :\frac{a}{2} = \sqrt 2 \tan \alpha
\end{array}\)



.png)











