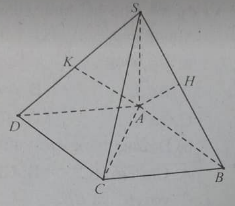
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Cắt hình lập phương bởi mặt phẳng trung trực của AC'. Thiết diện là hình gì?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai.png)
Ta có AC là hình chiếu của AC' lên (ABCD).
Mà \(AC \bot BD\) nên \(AC' \bot BD,{\rm{ }}(1)\)
Ta có \(\left. \begin{array}{l} AD \bot (AA'B'B)\\ A'B \subset (AA'B'B \end{array} \right\} \Rightarrow A'B \bot AD\)
Lại có \(A'B \bot AB'\) suy ra
\(\left. \begin{array}{l} A'B \bot (AB'C'D)\\ AC' \subset (AB'C'D) \end{array} \right\} \Rightarrow AC' \bot A'B,{\rm{ }}(2)\)
Từ (1) và (2) suy ra \(AC' \bot (A'BD),{\rm{ }}(3)\)
Mặt phẳng trung trực AC' là mặt phẳng \((\alpha)\) đi qua trung điểm I của AC' và \((\alpha ) \bot AC',{\rm{ }}(4)\)
Từ (3) và (4) suy ra \(\left\{ \begin{array}{l} mp(\alpha ){\rm{ qua }}I\\ (\alpha ){\rm{//}}(A'BD) \end{array} \right.\)
Do đó
Qua I dựng MQ // BD
Dựng \(\begin{array}{l} MN{\rm{//A'D}}\\ {\rm{NP//}}B'D'{\rm{//}}BD\\ QK{\rm{//B'C//A'D}}\\ KH{\rm{//}}BD \end{array}\)
Mà \(MN = NP = PQ = QK = KM = \frac{{a\sqrt 2 }}{2}\)
Suy ra thiết diện là lục giác đều.



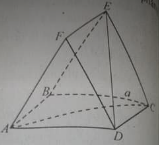
.png)