Cho hình lăng trụ lục giác đều ABCDEF.A'B'C'D'E'F' có cạnh bên bằng a và ADD'A' là hình vuông. Cạnh đáy của lăng trụ bằng:
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai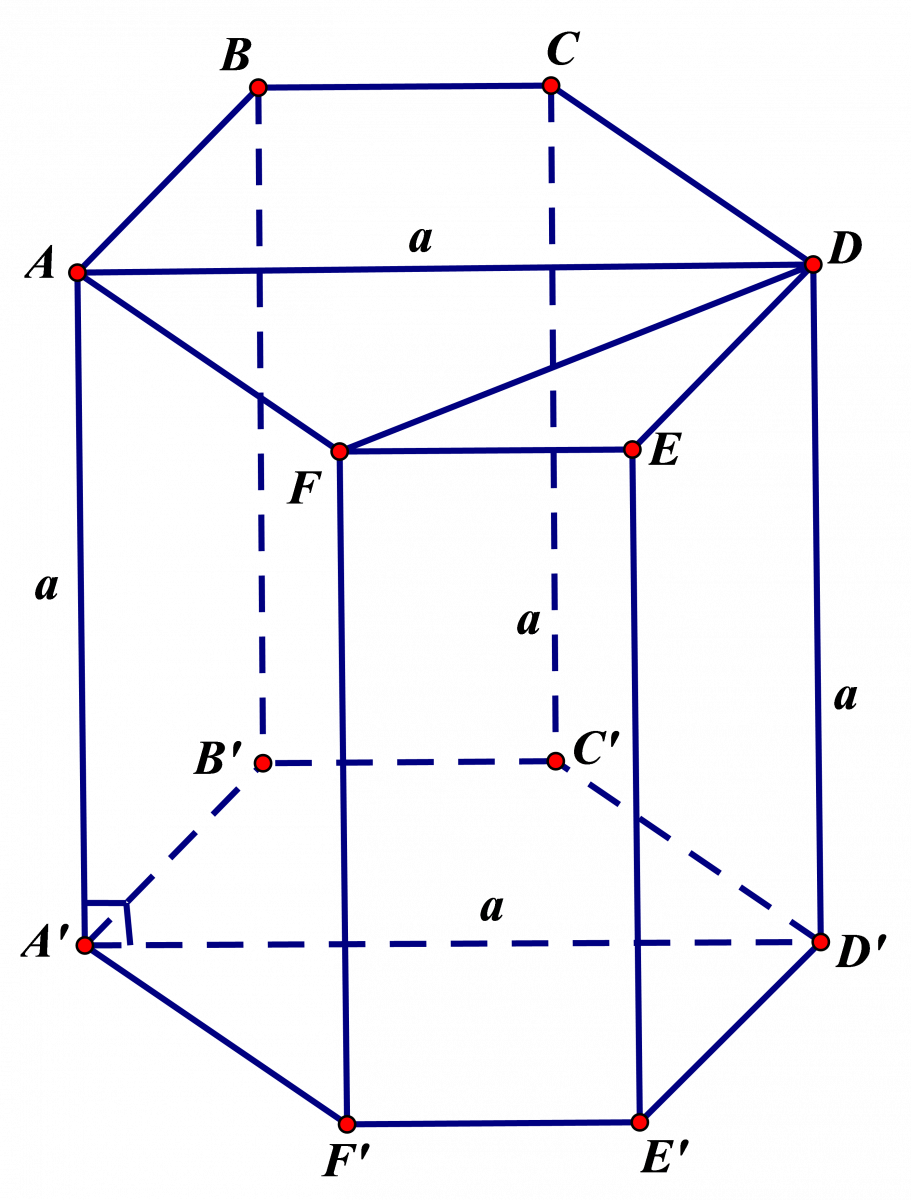
Tổng số đo các góc của hình lục giác là \(4.180^\circ = 720^\circ \).
Vì ABCDEF là hình lục giác đều nên mỗi góc của hình lục giác đều ABCDEF là 120o \( \Rightarrow \widehat {FAB} = 120^\circ \).
Vì ABCDEF là hình lục giác đều nên ta suy ra:
+ AD là tia phân giác của góc \(\widehat {FAB}\) và \(\widehat {EDC}\) \( \Rightarrow \widehat {FAD} = \frac{{\widehat {FAB}}}{2} = 60^\circ \)
+ Tam giác AFD vuông tại F.
Xét tam giác AFD vuông tại F có \(\widehat {FAD} = 60^\circ \) và AD = a ta suy ra:
\(\begin{array}{l} \cos \widehat {FAD} = \frac{{AF}}{{AD}}\\ \Rightarrow AF = AD.\cos \widehat {FAD} = a.\cos 60^\circ = a.\frac{1}{2} = \frac{a}{2}. \end{array}\)