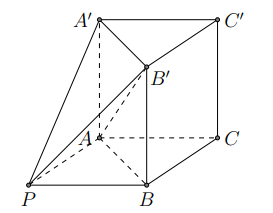
Cho hình lăng trụ đứng tam giác ABC:A0B0C0 có đáy ABC là tam giác cân, \(A B=A C=a, \widehat{B A C}=120^{\circ}\)cạnh bên \(A A^{\prime}=a \sqrt{2}\). Tính góc giữa hai đường thẳng AB' và BC.
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai
Dựng AP sao cho song song và bằng với CB như hình vẽ.
\(\begin{aligned} &\text { Suy ra }\widehat{(B C, A B^{\prime})}=\widehat{(A P, A B^{\prime})}\text { . }\\ &\text { Ta có } A P=C B=a \sqrt{3} \text { . }\\ &\text { Ta lại có } A B^{\prime}=\sqrt{B^{\prime} B^{2}+A B^{2}}=a \sqrt{3} ;\\ &B^{\prime} P=\sqrt{B^{\prime} B^{2}+P B^{2}}=a \sqrt{3}\\ &\text { Vậy } \triangle A P B^{\prime} \text { đều nên }\left(B C, A B^{\prime}\right)=\left(A P, A B^{\prime}\right)=60^{\circ} \text { . } \end{aligned}\)
Câu hỏi liên quan
-
Cho hình chóp cụt tứ giác đều ABCD.A'B'C'D' cạnh của đáy nhỏ ABCD bằng \(\frac{a}{3}\) và cạnh của đáy lớn A'B'C'D' bằng a. Góc giữa cạnh bên và mặt đáy bằng 60o. Tính chiều cao OO' của hình chóp cụt đã cho.
-
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Cắt hình lập phương bởi mặt phẳng trung trực của AC'. Diện tích thiết diện là
-
Cho tứ diện đều ABCD . Góc giữa (ABC) và (ABD) bằng \(\alpha\) . Chọn khẳng định đúng trong các khẳng định sau?
-
Cho hình chóp S.ABC có SA = SB = SC = AB = AC = 1, \(B C=\sqrt{2}\). Tính góc giữa hai đường thẳng AB, SC
-
Hình hộp ABCD.A'B'C'D' trở thành hình lăng trụ tứ giác đều khi phải thêm các điều kiện nào sau đây?
-
Cho hình chóp S.ABCD, đáy ABCD là hình vuông, \(SA \bot (ABCD)\). Gọi \((\alpha)\) là mặt phẳng chứa AB và vuông góc với (SCD), \((\alpha)\) cắt chóp S.ABCD theo thiết diện là hình gì?
-
Tứ diện đều ABCD cạnh a, M là trung điểm của cạnh CD. Cô-sin của góc giữa AM và BD là
-
Cho tứ diện ABCD có AC = AD và BC = BD. Gọi I là trung điểm của CD. Khẳng định nào sau đây sai ?
-
Cho tam giác ABC vuông tại A. Cạnh AB = a nằm trong mặt phẳng (P), cạnh \(AC = a\sqrt 2 \), AC tạo với (P) một góc 60o. Chọn khẳng định đúng trong các khẳng định sau?
-
Cho hình lăng trụ đứng ABC.A'B'C' có AB = AA' = a, BC = 2a, \(CA = a\sqrt 5 \). Khẳng định nào sau đây sai?
-
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Mặt phẳng (SAB) vuông góc với đáy (ABCD). Gọi H là trung điểm của AB, \(SH=HC,SA=AB\). Gọi \(\alpha \) là góc giữa đường thẳng SC và mặt phẳng (ABCD). Giá trị của \(\tan \alpha \) là:
-
Cho hình tứ diện ABCD có AB, BC, CD đôi một vuông góc. Mặt phẳng (ABD) vuông góc với mặt phẳng nào của tứ diện?
-
Cho hình chóp S.ABCD có hai mặt bên (SAB) và (SAC) vuông góc với mặt phẳng (ABC), tam giác ABC vuông cân ở A và có đường cao AH \(\left( {H \in BC} \right)\). Gọi O là hình chiếu vuông góc của A lên (SBC). Khẳng định nào sau đây sai ?
-
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, cạnh bên SA vuông góc với đáy, SA = a. Gọi M là trung điểm của SB. Góc giữa AM và BD bằng
-
Cho hình chóp S.ABCD có ABCD là hình chữ nhật. SA vuông góc với (ABCD), AH và AK lần lượt là đường cao của tam giác SAB và SAD.
Hai mặt phẳng (SAC) và (AHK) vuông góc vì:
.png)
-
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O và khoảng cách từ A đến BD bằng \(\frac{{2a}}{{\sqrt 5 }}\). Biết \(SA \bot \left( {ABCD} \right)\) và SA = 2a. Gọi \(\alpha\) là góc giữa hai mặt phẳng (ABCD) và (SBD). Khẳng định nào sau đây sai?
-
Cho hình lập phương \(ABCD.{A_1}{B_1}{C_1}{D_1}\). Gọi \(\alpha\) là góc giữa hai mặt phẳng \(\left( {{A_1}{D_1}CB} \right)\) và (ABCD). Chọn khẳng định đúng trong các khẳng định sau?
-
Trong các mệnh đề sau, mệnh đề nào đúng?
-
Cho hình chóp S.ABC có hai mặt bên (SBC) và (SAC) vuông góc với đáy (ABC). Khẳng định nào sau đây sai?
-
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, tâm của đáy là O. Gọi M và N lần lượt là trung điểm của SA và BC. Biết rằng góc giữa MN và (ABCD) bằng 60o, cosin góc giữa MN và mặt phẳng (SBD) bằng :
