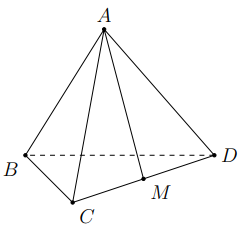
Cho tứ diện đều ABCD có M là trung điểm của cạnh CD , \(\varphi\) là góc giữa hai đường thẳng AM và BC. Giá trị \(\cos \varphi\) bằng
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai
Giả sử cạnh của tứ diện đều bằng a. Ta có:
\(\begin{array}{l} \overrightarrow{C B} \cdot \overrightarrow{A M}=\overrightarrow{C B} \cdot(\overrightarrow{C M}-\overrightarrow{C A}) \\ =\overrightarrow{C B} \cdot \overrightarrow{C M}-\overrightarrow{C B} \cdot \overrightarrow{C A} \\ =C B \cdot C M \cdot \cos \widehat{A C M}-C B \cdot C A \cdot \cos \widehat{A C B} \\ =C B \cdot C M \cdot \cos 60^{o}-C B \cdot C A \cdot \cos 60^{\circ} \\ =a \cdot \frac{a}{2} \cdot \frac{1}{2}-a \cdot a \cdot \frac{1}{2}=-\frac{1}{4} a^{2} \end{array}\)
Khi đó:
\(\cos \varphi=|\cos (\overrightarrow{B C}, \overrightarrow{A M})|=\left|\frac{\overrightarrow{B C} \cdot \overrightarrow{A M}}{B C \cdot A M}\right|=\frac{\sqrt{3}}{6}\)
Câu hỏi liên quan
-
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và SA = SB = SC = a.
Mặt phẳng (ABCD) vuông góc với mặt phẳng (SBD) vì:
-
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và đường cao SH bằng cạnh đáy. Tính số đo góc hợp bởi cạnh bên và mặt đáy.
-
Cho hai tam giác ACD và BCD nằm trên hai mặt phẳng vuông góc với nhau và AC = AD = BC = BD = a, CD = 2x. Gọi I, J lần lượt là trung điểm của AB và CD. Tính IJ theo a và x?
-
Cho tứ diện ABCD có AB vuông góc với mặt phẳng (BCD). Biết tam giác BCD vuông tại C và \(A B=\frac{a \sqrt{6}}{2}, A C=a \sqrt{2}, C D=a\). Gọi E là trung điểm của AD. Góc giữa hai đường thfẳng AB và CE bằng:
-
Cho hai tam giác ACD và BCD nằm trên hai mặt phẳng vuông góc với nhau và \(AC = AD = BC = BD = a;CD = 2x\). Với giá trị nào của x thì hai mặt phẳng (ABC) và (ABD) vuông góc.
-
Cho hình chóp S.ABC có hai mặt bên (SBC) và (SAC) vuông góc với đáy (ABC). Khẳng định nào sau đây sai ?
-
Cho tứ diện đều ABCD. Gọi M là trung điểm cạnh BC (tham khảo hình vẽ bên). Giá trị cô-sin của góc giữa hai đường thẳng AB và DM bằng
-
Cho tam giác ABC vuông tại A. Cạnh AB = a nằm trong mặt phẳng (P), cạnh \(AC = a\sqrt 2 \), AC tạo với (P) một góc 60o. Chọn khẳng định đúng trong các khẳng định sau?
-
Cho hình chóp S.ABCD có ABCD là hình chữ nhật. SA vuông góc với (ABCD), AH và AK lần lượt là đường cao của tam giác SAB và SAD.
Hai mặt phẳng (SAB) và (SBC) vuông góc vì.
-
Cho hình chóp S ABCD . có đáy ABCD là hình vuông tâm O . Biết \(S O \perp(A B C D)\), \(S O=a \sqrt{3}\) và đường tròn ngoại tiếp ABCD có bán kính bằng a . Gọi \(\alpha\) là góc hợp bởi mặt bên (SCD) với đáy. Khi đó \(\tan \alpha=?\)
-
Cho hình lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình thoi, AC = 2a. Các cạnh bên vuông góc với đáy và AA' = a. Khẳng định nào sau đây sai ?
-
Cho tứ diện ABCD có \(AB \bot \left( {BCD} \right)\). Trong \(\Delta BCD\) vẽ các đường cao BE và DF cắt nhau ở O. Trong (ADC) vẽ \(DK \bot AC\) tại K. Khẳng định nào sau đây sai ?
-
Cho hình lăng trụ ABCD.A'B'C'D'. Hình chiếu vuông góc của A' lên (ABC) trùng với trực tâm H của tam giác ABC. Khẳng định nào sau đây không đúng?
-
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA ⊥ (ABC) và SA = a/2.
Góc giữa hai mặt phẳng (SAB) và (SAC) bằng:
.png)
-
Cho tứ diện ABCD có: AB = AC = AD, góc BAC bằng góc BAD bằng 60o. Gọi M và N lần lượt là trung điểm của AB và CD.
Đường vuông góc chung của AB và CD là:
-
Cho hình chóp S,ABC có \(SA \bot \left( {ABC} \right)\) và \(AB \bot BC\), gọi I là trung điểm BC. Góc giữa hai mặt phẳng (SBC) và (ABC) là góc nào sau đây?
-
Trong các mệnh đề sau, mệnh đề nào đúng?
-
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh BC và AD. Biết \(A B=C D=2 a, M N=a \sqrt{3}\). Tính góc giữa hai đường thẳng AB và CD
-
Trong các mệnh đề sau, mệnh đề nào sai?
-
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Mặt phẳng (SAB) vuông góc với đáy (ABCD). Gọi H là trung điểm của AB, \(SH=HC,SA=AB\). Gọi \(\alpha \) là góc giữa đường thẳng SC và mặt phẳng (ABCD). Giá trị của \(\tan \alpha \) là:
