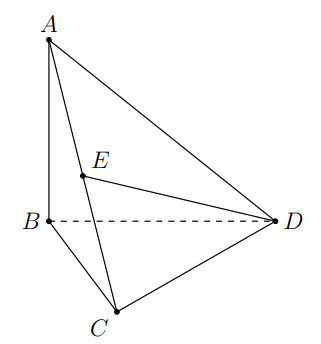
Cho hình chóp tứ giác S.ABCD, có đáy ABCD là hình thoi tâm I cạnh bằng a và góc \(\widehat A = {60^0}\), cạnh \(SC = \frac{{a\sqrt 6 }}{2}\) và SC vuông góc với mặt phẳng (ABCD). Trong tam giác SCA kẻ \(IK \bot SA\) tại K. Tính độ dài IK được
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai.png)
Tam giác AKI đồng dạng tam giác ACS \( \Rightarrow \frac{{IK}}{{SC}} = \frac{{AI}}{{SA}} \Rightarrow IK = \frac{{SC.AI}}{{SA}}\)
\(\Delta BCD\) và \(\Delta ABD\) đều cạnh \(a \Rightarrow IA = IC = \frac{{a\sqrt 3 }}{2} \Rightarrow AC = a\sqrt 3 \)
\(\Delta SAC\) vuông tại \(C \Rightarrow SA = \sqrt {S{C^2} + A{C^2}} = \sqrt {{{\left( {\frac{{a\sqrt 6 }}{2}} \right)}^2} + {{\left( {a\sqrt 3 } \right)}^2}} = \frac{{3a\sqrt 2 }}{2}\)
Vậy \(IK = \frac{a}{2}\)