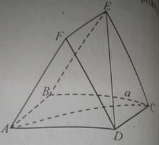
Cho hình chóp cụt tứ giác đều ABCD.A'B'C'D' cạnh của đáy nhỏ ABCD bằng \(\frac{a}{3}\) và cạnh của đáy lớn A'B'C'D' bằng a. Góc giữa cạnh bên và mặt đáy bằng 60o. Tính chiều cao OO' của hình chóp cụt đã cho.
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai.png)
Ta có \(SO' \bot \left( {A'B'C'D'} \right) \supset B'D' \Rightarrow SO' \bot B'D'\)
⇒ O'D' là hình chiếu vuông góc của SD' lên (A'B'C'D').
\( \Rightarrow \left( {SD',\left( {ABCD} \right)} \right) = \left( {SD',O'D'} \right) = \widehat {SD'O'} = 60^\circ \)
Từ giả thiết dễ dàng chỉ ra được \(\frac{{AA'}}{{SA'}} = \frac{{OO'}}{{SO'}} = \frac{1}{3}\).
Vì \(\Delta A'D'C'\) là tam giác vuông cân tại D' có D'O' là đường cao nên ta có:
\(\frac{1}{{D'{{O'}^2}}} = \frac{1}{{A'{{D'}^2}}} + \frac{1}{{D'{{C'}^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{{a^2}}} = \frac{2}{{{a^2}}}\)
\(\Rightarrow D'{O'^2} = \frac{{{a^2}}}{2}\)
\(\Rightarrow D'O' = \frac{{a\sqrt 2 }}{2}\)
Áp dụng hệ thức lượng trong \(\Delta SD'O'\) vuông tại O' ta có:
\(\tan 60^\circ = \frac{{SO'}}{{O'D'}}\)
\(\Rightarrow SO' = O'D'.\tan 60^\circ = \frac{{a\sqrt 2 }}{2}.\sqrt 3 = \frac{{a\sqrt 6 }}{2}\)
\( \Rightarrow OO' = \frac{1}{3}SO' = \frac{1}{3}.\frac{{a\sqrt 6 }}{2} = \frac{{a\sqrt 6 }}{6}\)
Câu hỏi liên quan
-
Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a. Khẳng định nào sau đây sai?
-
Cho các mệnh đề sau với \((\alpha) \text { và }(\beta)\) là hai mặt phẳng vuông góc với nhau với giao tuyến \(m=(\alpha) \cap(\beta) \) và a, b, c, d là các đường thẳng. Các mệnh đề sau, mệnh đề nào đúng?
-
Cho hình chóp S.ABC có \(S A \perp(A B C)\) và đáy ABC vuông ở A . Khẳng định nào sau đây sai ?
-
Cho hình lăng trụ ABCD.A'B'C'D'. Hình chiếu vuông góc của A' lên (ABC) trùng với trực tâm H của tam giác ABC. Khẳng định nào sau đây không đúng?
-
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. \(SA \bot \left( {ABCD} \right)\), SA = x. Xác định x để hai mặt phẳng (SBC) và (SCD) tạo với nhau góc 60o.
-
Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Biết thể tích của hình chóp S.ABCD là \(\frac{{{a}^{3}}\sqrt{15}}{6}\). Góc giữa đường thẳng SC và mặt phẳng đáy (ABCD) là:
-
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA ⊥ (ABC) và SA = a/2.
M là trung điểm của BC. Khi đó góc giữa hai mặt phẳng (SAM) và (SBC) bằng:
-
Cho hình hộp ABCD.A'B'C'D' có AB = a, BC = b, CC' = c. Nếu \(AC' = BD' = B'D = \sqrt {{a^2} + {b^2} + {c^2}} \) thì hình hộp là
-
Trong các mệnh đề sau, mệnh đề nào đúng?
-
Cho tam giác ABC vuông tại A. Cạnh AB = a nằm trong mặt phẳng (P), cạnh \(AC = a\sqrt 2 \), AC tạo với (P) một góc 60o. Chọn khẳng định đúng trong các khẳng định sau?
-
Cho hình chóp S.ABC có hai mặt bên (SBC) và (SAC) vuông góc với đáy (ABC). Khẳng định nào sau đây sai ?
-
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O. Biết \(SO \bot \left( {ABCD} \right),SO = a\sqrt 3 \) và đường tròn nội tiếp ABCD có bán kính bằng a. Tính góc hợp bởi mỗi mặt bên với đáy.
-
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = AA' = a, AD = 2a. Gọi \(\alpha\) là góc giữa đường chéo A'C và đáy ABCD. Tính \(\alpha\).
-
Cho tứ diện ABCD có AB vuông góc với mặt phẳng (B C D). Biết tam giác BCD vuông tại C và \(A B=\frac{a \sqrt{6}}{2}, A C=a \sqrt{2}, C D=a\). Gọi E là trung điểm của AC (tham khảo hình vẽ bên). Góc giữa hai đường thẳng A B và DE bằng
-
Cho hình chóp S ABCD . có đáy ABCD là hình vuông tâm O . Biết \(S O \perp(A B C D)\), \(S O=a \sqrt{3}\) và đường tròn ngoại tiếp ABCD có bán kính bằng a . Gọi \(\alpha\) là góc hợp bởi mặt bên (SCD) với đáy. Khi đó \(\tan \alpha=?\)
-
Cho hai tam giác ACD và BCD nằm trên hai mặt phẳng vuông góc với nhau và \(AC = AD = BC = BD = a;CD = 2x\). Với giá trị nào của x thì hai mặt phẳng (ABC) và (ABD) vuông góc.
-
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và có SA = SB = SC = a. Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng
-
Cho hình chóp tam giác đều S. ABC có độ dài cạnh đáy bằng a. Độ dài cạnh bên của hình chóp bằng bao nhiêu để góc giữa cạnh bên và mặt đáy bằng 600 ?
-
Cho hình lập phương \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}\) . Góc giữa \(A^{\prime} C^{\prime} \text { và } D^{\prime} C^{\prime}\) là
-
Cho hình lăng trụ đứng \(ABC.ABC\) có đáy là tam giác cân với \(AB=AC=a,\) góc \(\widehat{ABC}={{120}^{0}},\) cạnh bên BB’ = a. Gọi I là trung điểm của CC’. Tính cosin của góc giữa hai mặt phẳng (ABC) và (AB’I)?
