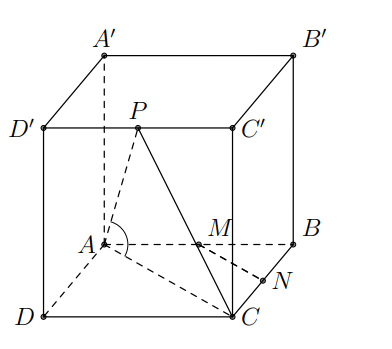
Cho hình lập phương \(A B C D . A^{\prime} B^{\prime} C^{\prime} D^{\prime}\) cạnh a.Gọi M, N, P lần lượt là trung điểm các cạnh A B, B C, C'D'. Xác định góc giữa hai đường thẳng MN và AP.
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai
Do AC song song với MN nên góc giữa hai đường thẳng MN và AP bằng góc giữa hai đường thẳng AC và AP.
Tính được \(P C=\frac{a \sqrt{5}}{2} ; A P=\frac{3 a}{2} ; A C=a \sqrt{2} .\)
Áp dụng định lý cosin cho tam giác ACP ta có
\(\begin{array}{l} \cos \widehat{C A P}=\frac{A P^{2}+A C^{2}-P C^{2}}{2 A P \cdot A C}=\frac{\frac{9 a^{2}}{4}+2 a^{2}-\frac{5 a^{2}}{4}}{2 \cdot \frac{3 a}{2} \cdot a \sqrt{2}}=\frac{\sqrt{2}}{2} \\ \Rightarrow \widehat{C A P}=45^{\circ} . \end{array}\)
Câu hỏi liên quan
-
Cho tam giác ABC và mặt phẳng (P). Biết góc giữa mặt phẳng (P) và mặt phẳng (ABC) là \(\varphi \). Hình chiếu của tam giác ABC trên mặt phẳng (P) là tam giác A'B'C'. Tìm hệ thức liên hệ giữa diện tích tam giác ABC và diện tích tam giác A'B'C'.
-
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA ⊥ (ABC) và SA = a/2.
Góc giữa hai mặt phẳng (SAB) và (ABC) bằng:
-
Hình hộp ABCD.A'B'C'D' trở thành hình lăng trụ tứ giác đều khi phải thêm các điều kiện nào sau đây?
-
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và có SA = SB = SC = a. Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng
-
Cho hai tam giác ACD và BCD nằm trên hai mặt phẳng vuông góc với nhau và AC = AD = BC = BD = a, CD = 2x. Tính AB theo a và x?
-
Cho hình chóp S.ABC có \(SA \bot \left( {ABC} \right)\) và đáy ABC vuông ở A. Khẳng định nào sau đây sai?
-
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và SA = SB = SC = a.
Góc giữa mặt bên hình chóp S.ABCD và mặt phẳng đáy có tang bằng:
-
Cho hai tam giác ACD và BCD nằm trên hai mặt phẳng vuông góc với nhau và \(AC = AD = BC = BD = a;CD = 2x\). Với giá trị nào của x thì hai mặt phẳng (ABC) và (ABD) vuông góc.
-
Cho hình lập phương \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}\). Góc giữa hai đường thẳng AC và A'D bằng
-
Cho hình chóp tam giác đều S. ABC có độ dài cạnh đáy bằng a. Độ dài cạnh bên của hình chóp bằng bao nhiêu để góc giữa cạnh bên và mặt đáy bằng 600 ?
-
Cho tứ diện OABC có OA,OB,OC đôi một vuông góc với nhau và OA=OB=OC. Gọi M là trung điểm của BC (tham khảo hình vẽ bên). Góc giữa hai đường thẳng OM và AB bằng
-
Cho hình lăng trụ tứ giác đều ABCD.A'B'C'D' có ACC'A' là hình vuông, cạnh bằng a. Cạnh đáy của hình lăng trụ bằng:
-
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và góc \(\widehat {ABC} = {60^0}\). Các cạnh SA, SB, SC đều bằng \(a\frac{{\sqrt 3 }}{2}\). Gọi \(\varphi \) là góc của hai mặt phẳng (SAC) và (ABCD). Giá trị \(\tan \varphi \) bằng bao nhiêu?
-
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O. Biết \(SO \bot \left( {ABCD} \right),SO = a\sqrt 3 \) và đường tròn nội tiếp ABCD có bán kính bằng a. Tính góc hợp bởi mỗi mặt bên với đáy.
-
Tính cosin của góc giữa hai mặt của một tứ diện đều.
-
Trong các mệnh đề sau, mệnh đề nào đúng?
-
Cho hình lập phương \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}\) . Góc giữa \(A^{\prime} C^{\prime} \text { và } D^{\prime} C^{\prime}\) là
-
Cho hai mặt phẳng vuông góc (P) và (Q) có giao tuyến \(\Delta\). Lấy A, B cùng thuộc \(\Delta\) và lấy C trên (P), D trên (Q) sao cho \(AC \bot AB,BD \bot AB\) và AB = AC = BD. Thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng \((\alpha)\) đi qua A và vuông góc với CD là hình gì?
-
Cho hình chóp tứ giác đều S.ABCD, có đáy ABCD là hình vuông tâm O. Các cạnh bên và các cạnh đáy đều bằng A. Gọi M là trung điểm SC. Góc giữa hai mặt phẳng (MBD) và (ABCD) bằng:
-
Cho tứ diện ABCD có \(A C=A D \text { và } B C=B D\) . Gọi I là trung điểm của CD . Khẳng định nào sau đây sai?
