Trắc nghiệm Hai mặt phẳng vuông góc Toán Lớp 11
-
Câu 1:
Cho hình chóp tứ giác đều S.ABCD có SA = SB. Góc giữa (SAB) và (SAD) bằng αα. Chọn khẳng định đúng trong các khẳng định sau?
A. cosα=−13cosα=−13
B. cosα=25cosα=25
C. α=600α=600
D. cosα=23cosα=23
-
Câu 2:
Tính cosin của góc giữa hai mặt của một tứ diện đều.
A. 13.13.
B. 12.12.
C. √23.√23.
D. √32.√32.
-
Câu 3:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông có tâm O và SA⊥(ABCD)SA⊥(ABCD). Khẳng định nào sau đây sai ?
A. Góc giữa hai mặt phẳng (SBC) và (ABCD) là góc ^ABSˆABS.
B. (SAC)⊥(SBD)(SAC)⊥(SBD)
C. Góc giữa hai mặt phẳng (SBD) và (SBCD) là góc ^SOAˆSOA.
D. Góc giữa hai mặt phẳng (SAD) và (ABCD) là góc ^SDAˆSDA.
-
Câu 4:
Cho hình lập phương ABCD.A1B1C1D1ABCD.A1B1C1D1. Gọi αα là góc giữa hai mặt phẳng (A1D1CB)(A1D1CB) và (ABCD). Chọn khẳng định đúng trong các khẳng định sau?
A. α=450α=450
B. α=300α=300
C. α=600α=600
D. α=900α=900
-
Câu 5:
Cho hình lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình thoi, AC = 2a. Các cạnh bên vuông góc với đáy và AA' = a. Khẳng định nào sau đây sai ?
A. Các mặt bên của hình lăng trụ là các hình chữ nhật.
B. Góc giữa hai mặt phẳng (AA'C'C) và (BB'D'D) có số đo bằng 60o.
C. Hai mặt bên (AA'C) và (BB'C) vuông góc với hai đáy.
D. Hai hai mặt bên (AA'B'B) và (AA'D'D) bằng nhau.
-
Câu 6:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O và khoảng cách từ A đến BD bằng 2a√52a√5. Biết SA⊥(ABCD)SA⊥(ABCD) và SA = 2a. Gọi αα là góc giữa hai mặt phẳng (ABCD) và (SBD). Khẳng định nào sau đây sai?
A. (SAB)⊥(SAD)(SAB)⊥(SAD)
B. (SAC)⊥(ABCD)(SAC)⊥(ABCD)
C. tanα=√5tanα=√5
D. α=^SOAα=ˆSOA
-
Câu 7:
Trong không gian cho tam giác đều SAB và hình vuông ABCD cạnh a nằm trên hai mặt phẳng vuông góc. Gọi H, K lần lượt là trung điểm của AB, CD. Ta có tan của góc tạo bởi hai mặt phẳng (SAB) và (SCD) bằng :
A. √23√23
B. 2√332√33
C. √33√33
D. √32√32
-
Câu 8:
Cho hình chóp tam giác đều S.ABC với SA = 2AB. Góc giữa (SAB) và (ABC) bằng a. Chọn khẳng định đúng trong các khẳng định sau?
A. α=600α=600
B. cosα=13√5cosα=13√5
C. cosα=14√5cosα=14√5
D. cosα=12√5cosα=12√5
-
Câu 9:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O. Biết SO⊥(ABCD)SO⊥(ABCD), SO=a√3SO=a√3 và đường tròn ngoại tiếp ABCD có bán kính bằng a. Gọi αα là góc hợp bởi mặt bên (SCD) với đáy. Khi đó tanα=?tanα=?
A. √32√32
B. √3√2√3√2
C. √66√66
D. √6√6
-
Câu 10:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA⊥(ABCD)SA⊥(ABCD), gọi O là tâm hình vuông ABCD. Khẳng định nào sau đây sai?
A. Góc giữa hai mặt phẳng (SBC) và (ABCD) là ^ABSˆABSgóc .
B. Góc giữa hai mặt phẳng (SBD) và (ABCD) là góc ^SOAˆSOA.
C. Góc giữa hai mặt phẳng (SAD) và (ABCD) là góc ^SDAˆSDA.
D. (SAC)⊥(SBD)(SAC)⊥(SBD)
-
Câu 11:
Cho hình chóp S,ABC có SA⊥(ABC)SA⊥(ABC) và AB⊥BCAB⊥BC, gọi I là trung điểm BC. Góc giữa hai mặt phẳng (SBC) và (ABC) là góc nào sau đây?
A. Góc SBA
B. Góc SCA
C. Góc SCB
D. Góc SIA
-
Câu 12:
Cho tứ diện ABCD có AC = AD và BC = BD. Gọi I là trung điểm của CD. Khẳng định nào sau đây sai ?
A. Góc giữa hai mặt phẳng (ACD) và (BCD) là góc ^AIBˆAIB.
B. (BCD)⊥(AIB)(BCD)⊥(AIB)
C. Góc giữa hai mặt phẳng (ABC) và (ABD) là góc ^CBDˆCBD.
D. (ACD)⊥(AIB)(ACD)⊥(AIB)
-
Câu 13:
Cho hình chóp S.ABC có SA⊥(ABC)SA⊥(ABC) và đáy ABC vuông ở A. Khẳng định nào sau đây sai?
A. (SAB)⊥(ABC)(SAB)⊥(ABC)
B. (SAB)⊥(SAC)(SAB)⊥(SAC)
C. Vẽ AH⊥BC,H∈BC⇒AH⊥BC,H∈BC⇒ góc AHS là góc giữa hai mặt phẳng (SBC) và (ABC).
D. Góc giữa hai mặt phẳng (SBC) và (SAC) là góc ^SCBˆSCB.
-
Câu 14:
Cho tam giác ABC vuông tại A. Cạnh AB = a nằm trong mặt phẳng (P), cạnh AC=a√2AC=a√2, AC tạo với (P) một góc 60o. Chọn khẳng định đúng trong các khẳng định sau?
A. (ABC) tạo với (P) góc 45o
B. BC tạo với (P) góc 30o
C. BC tạo với (P) góc 45o
D. BC tạo với (P) góc 60o
-
Câu 15:
Cho hình chóp tứ giác đều S.ABCD, có đáy ABCD là hình vuông tâm O. Các cạnh bên và các cạnh đáy đều bằng A. Gọi M là trung điểm SC. Góc giữa hai mặt phẳng (MBD) và (ABCD) bằng:
A. 90o
B. 60o
C. 45o
D. 30o
-
Câu 16:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và có SA = SB = SC = a. Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng
A. 30o
B. 90o
C. 60o
D. 45o
-
Câu 17:
Cho hình chóp S.ABCD có đáy là hình thoi tâm O cạnh a và có góc ^BAD=600ˆBAD=600. Đường thẳng SO vuông góc với mặt phẳng đáy (ABCD) và SO=3a4SO=3a4. Gọi E là trung điểm BC và F là trung điểm BE. Góc giữa hai mặt phẳng (SOF) và (SBC) là
A. 90o
B. 60o
C. 30o
D. 45o
-
Câu 18:
Cho hình chóp S.ABCD có hai mặt bên (SAB) và (SAC) vuông góc với mặt phẳng (ABC), tam giác ABC vuông cân ở A và có đường cao AH (H∈BC)(H∈BC). Gọi O là hình chiếu vuông góc của A lên (SBC). Khẳng định nào sau đây sai ?
A. SC⊥(ABC)SC⊥(ABC)
B. O∈SHO∈SH
C. (SAH)⊥(SBC)(SAH)⊥(SBC)
D. (^(SBC),(ABC))=^SBA(ˆ(SBC),(ABC))=ˆSBA
-
Câu 19:
Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng a. Tính của góc giữa một mặt bên và một mặt đáy.
A. 1212
B. $\frac{1}{3}$
C. 1√31√3
D. 1√21√2
-
Câu 20:
Cho tứ diện đều ABCD. Góc giữa (ABC) và (ABD) bằng αα. Chọn khẳng định đúng trong các khẳng định sau?
A. cosα=13cosα=13
B. cosα=14cosα=14
C. α=600α=600
D. cosα=15cosα=15
-
Câu 21:
Cho hình chóp tứ giác S.ABCD, có đáy ABCD là hình thoi tâm I cạnh bằng a và góc ˆA=600ˆA=600, cạnh SC=a√62SC=a√62 và SC vuông góc với mặt phẳng (ABCD). Trong tam giác SAC kẻ IK⊥SAIK⊥SA tại K. Tính số đo góc ^BKDˆBKD.
A. 60o
B. 45o
C. 90o
D. 30o
-
Câu 22:
Cho tứ diện ABCD có AC = AD và BC = BD. Gọi I là trung điểm của CD. Khẳng định nào sau đây sai?
A. Góc giữa hai mặt phẳng (ABC) và (ABD) là ^CBDˆCBD.
B. Góc giữa hai mặt phẳng (ACD) và (BCD) là ^AIBˆAIB.
C. (BCD)⊥(AIB)(BCD)⊥(AIB)
D. (ACD)⊥(AIB)(ACD)⊥(AIB)
-
Câu 23:
Trong các mệnh đề sau, mệnh đề nào sai?
A. Hình lăng trụ tam giác có hai mặt bên là hình chữ nhật là hình lăng trụ đứng.
B. Hình chóp có đáy là đa giác đều và có các cạnh bên bằng nhau là hình chóp đều.
C. Hình lăng trụ đứng có đáy là đa giác đều là hình lăng trụ đều.
D. Hình lăng trụ có đáy là đa giác đều là hình lăng trụ đều.
-
Câu 24:
Hình hộp ABCD.A'B'C'D' là hình hộp gì nếu tứ diện AA'B'D' có các cạnh đối vuông góc.
A. Hình lập phương.
B. Hình hộp tam giác.
C. Hình hộp thoi.
D. Hình hộp tứ giác.
-
Câu 25:
Trong các mệnh đề sau, mệnh đề nào đúng?
A. Nếu hình hộp có hai mặt là hình chữ nhật thì nó là hình hộp chữ nhật.
B. Nếu hình hộp có năm mặt là hình chữ nhật thì nó là hình hộp chữ nhật.
C. Nếu hình hộp có bốn mặt là hình chữ nhật thì nó là hình hộp chữ nhật.
D. Nếu hình hộp có ba mặt là hình chữ nhật thì nó là hình hộp chữ nhật.
-
Câu 26:
Trong lăng trụ đều, khẳng định nào sau đây sai?
A. Đáy là đa giác đều.
B. Các mặt bên là những hình chữ nhật nằm trong mặt phẳng vuông góc với đáy.
C. Các cạnh bên là những đường cao.
D. Các mặt bên là những hình bình hành.
-
Câu 27:
Trong các mệnh đề sau, mệnh đề nào đúng?
A. Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.
B. Có duy nhất một mặt phẳng đi qua một đường thẳng cho trước và vuông góc với một mặt phẳng cho trước.
C. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
D. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.
-
Câu 28:
Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai đường thẳng không cắt nhau, không song song thì chéo nhau.
B. Hai đường thẳng không cắt nhau, không song song thì chéo nhau.
C. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song.
D. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song.
-
Câu 29:
Mệnh đề nào sau đây là đúng?
A. Hai mặt phẳng vuông góc với nhau thì mọi đường thẳng nằm trong mặt phẳng này sẽ vuông góc với mặt phẳng kia.
B. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì vuông góc với nhau.
C. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
D. Hai mặt phẳng vuông góc với nhau thì mọi đường thẳng nằm trong mặt phẳng này và vuông góc với giao tuyến của hai mặt phẳng sẽ vuông góc với mặt phẳng kia.
-
Câu 30:
Chỉ ra mệnh đề đúng trong các mệnh đề sau:
A. Cho hai đường thẳng song song a và b và đường thẳng c sao cho c⊥a,c⊥bc⊥a,c⊥b. Mọi mặt phẳng (α)(α) chứa c thì đều vuông góc với mặt phẳng (a,b).
B. Cho a⊥(α)a⊥(α), mọi mặt phẳng (β)(β) chứa a thì (β)⊥(α)(β)⊥(α).
C. Cho a⊥ba⊥b, mọi mặt phẳng chứa b đều vuông góc với a.
D. Cho a⊥ba⊥b, nếu a⊂(α)a⊂(α) và b⊂(β)b⊂(β) thì (α)⊥(β)(α)⊥(β).
-
Câu 31:
Cho các mệnh đề sau với (α)(α) và (β)(β) là hai mặt phẳng vuông góc với nhau với giao tuyến m=(α)∩(β)m=(α)∩(β) và a, b, c, d là các đường thẳng. Các mệnh đề sau, mệnh đề nào đúng?
A. Nếu b⊥mb⊥m thì b⊂(α)b⊂(α) hoặc b⊂(β)b⊂(β)
B. Nếu b⊥mb⊥m thì d⊥(α)d⊥(α).
C. Nếu a⊂(α)a⊂(α) và a⊥ma⊥m thì a⊥(β)a⊥(β)
D. Nếu c // m thì c//(α)c//(α) hoặc c//(β)c//(β)
-
Câu 32:
Cho hai đường thẳng chéo nhau a và b đồng thời a⊥ba⊥b. Chỉ ra mệnh đề đúng trong các mệnh đề sau:
A. mặt phẳng (Q) chứa b và đường vuông góc chung của a và b thì mp(Q)⊥amp(Q)⊥a.
B. mặt phẳng (R) chứa b và chứa đường thẳng b′⊥a thì mp(R)⊥a.
C. mặt phẳng (α) chứa a, mp (β) chứa b thì (α)⊥(β).
D. mặt phẳng (P) chứa b thì mặt phẳng (P)⊥a.
-
Câu 33:
Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai mặt phẳng cùng song song với một mặt phẳng thứ ba thì song song với nhau.
B. Qua một đường thẳng cho trước có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.
C. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với hai mặt phẳng cắt nhau cho trước.
D. Hai mặt phẳng cùng vuông góc với một mặt phẳng thứ ba thì vuông góc với nhau.
-
Câu 34:
Trong các mệnh đề sau, mệnh đề nào sai?
A. Cho đường thẳng a vuông góc với đường thẳng b và b nằm trong mặt phẳng (P). Mọi mặt phẳng (Q) chứa a và vuông góc với b thì (P) vuông góc với (Q).
B. Nếu đường thẳng a vuông góc với đường thẳng b và mặt phẳng (P) chứa a, mặt phẳng (Q) chứa b thì (P) vuông góc với (Q).
C. Cho đường thẳng a vuông góc với mặt phẳng (P) mọi mặt phẳng (Q) chứa a thì (P) vuông góc với (Q)
D. Cho đường thẳng vuông góc với mặt phẳng mọi mặt phẳng chứa thì vuông góc với
-
Câu 35:
Trong các mệnh đề sau, mệnh đề nào sai?
A. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
B. Qua một đường thẳng có duy nhất một mặt phẳng vuông góc với một đường thẳng cho trước.
C. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
D. Qua một đường thẳng có duy nhất một mặt phẳng vuông góc với một đường thẳng cho trước.
-
Câu 36:
Trong các mệnh đề sau đây, mệnh đề nào là đúng?
A. Một mặt phẳng (α) và một đường thẳng a không thuộc (α) cùng vuông góc với đường thẳng b thì (α) song song với a
B. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì vuông góc với nhau.
C. Hai mặt phẳng cùng vuông góc với một mặt phẳng thì cắt nhau.
D. Hai đường thẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau
-
Câu 37:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA ⊥ (ABC) và SA = a/2.
Góc giữa hai mặt phẳng (SAB) và (SAC) bằng:
.png)
A. 00
B. 450
C. 600
D. 900
-
Câu 38:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA ⊥ (ABC) và SA = a/2.
M là trung điểm của BC. Khi đó góc giữa hai mặt phẳng (SAM) và (SBC) bằng:
A. 00
B. 300
C. 450
D. 600
-
Câu 39:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA ⊥ (ABC) và SA = a/2.
Góc giữa hai mặt phẳng (SAB) và (ABC) bằng:
A. 00
B. 450
C. 600
D. 900
-
Câu 40:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và SA = SB = SC = a.
Mặt phẳng (ABCD) vuông góc với mặt phẳng (SBD) vì:
A. AC ⊂ (SAC) và AC ⊥ (SBD) do AC ⊥ SO và AC ⊥ BD
B. AC ⊂ (ABCD) và AC ⊥ (SBD) do AC ⊥ SO và AC ⊥ BD
C. AC ⊂ (SAC) và AC ⊥ SO ⊂ (SBD)
D. AC ⊂ (ABCD) và AC ⊥ SO ⊂ (SBD) và góc AOS bằng 90o
-
Câu 41:
Cho hình tứ diện ABCD có AB, BC, CD đôi một vuông góc. Mặt phẳng (ABD) vuông góc với mặt phẳng nào của tứ diện?
A. Không vuông góc với mặt nào
B. (ACD)
C. (ABC)
D. (BCD)
-
Câu 42:
Cho hình lập phương ABCD.A’B’C’D’. Mặt phẳng (ACC’A’) Không vuông góc với?
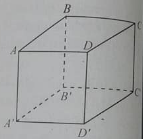
A. (ABCD)
B. (CDD’C’)
C. (BDC’)
D. (A’BD)
-
Câu 43:
Cho tứ diện ABCD có: AB = AC = AD, góc BAC bằng góc BAD bằng 60o. Gọi M và N lần lượt là trung điểm của AB và CD.
Đường vuông góc chung của AB và CD là:
A. BN
B. AN
C. BC
D. MN
-
Câu 44:
Cho tứ diện ABCD có: AB = AC = AD, góc BAC bằng góc BAD bằng 60o60o. Gọi M và N lần lượt là trung điểm của AB và CD.
Mặt phẳng (BCD) vuông góc với mặt phẳng
A. (CDM)
B. (ACD)
C. (ABN)
D. (ABC)
-
Câu 45:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và SA = SB = SC = a.
Góc giữa mặt bên hình chóp S.ABCD và mặt phẳng đáy có tang bằng:
A. 1
B. √3
C. √32
D. Đáp án khác
-
Câu 46:
Cho tứ diện ABCD có: AB = AC = AD, góc BAC bằng góc BAD bằng 60o. Gọi M và N lần lượt là trung điểm của AB và CD.
Góc giữa hai mặt phẳng (ACD) và (BCD) là:
A. ^ACB
B. ^ANB
C. ^ADB
D. ^MNB
-
Câu 47:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và SA = SB = SC = a.
Mặt phẳng (ABCD) vuông góc với mặt phẳng:
A. (SAD)
B. (SBD)
C. (SDC)
D. (SBC)
-
Câu 48:
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và góc giữa cạnh bên với mặt phẳng đáy bằng ∝
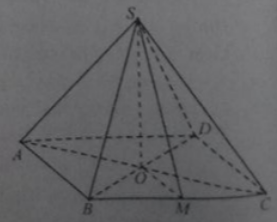
Tan của góc giữa mặt bên và mặt đáy bằng:
A. tanα
B. cotα
C. √2tanα
D. √22tanα
-
Câu 49:
Cho hai hình vuông ABCD và ABEF cạnh a nằm trên hai mặt phẳng vuông góc. Đường thẳng DE vuông góc?
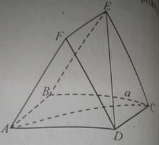
A. Chỉ với AC
B. Chỉ với BF
C. Chỉ với AC và BF
D. Hoặc với AC hoặc với BF
-
Câu 50:
Cho hai hình vuông ABCD và ABEF cạnh a nằm trên hai mặt phẳng vuông góc. Tính DE.
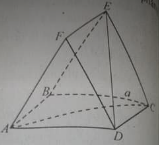
A. a√3
B. a√2
C. 3a2
D. a(1+√3)














