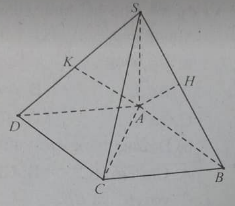
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O và khoảng cách từ A đến BD bằng \(\frac{{2a}}{{\sqrt 5 }}\). Biết \(SA \bot \left( {ABCD} \right)\) và SA = 2a. Gọi \(\alpha\) là góc giữa hai mặt phẳng (ABCD) và (SBD). Khẳng định nào sau đây sai?

Cho hình lăng trụ tam giác đều \(A B C . A^{\prime} B^{\prime} C^{\prime} \text { có } A B=a\,và\,A A^{\prime}=\sqrt{2} a\). Góc giữa hai đường thẳng AB' và BC' bằng

Mệnh đề nào sau đây là đúng?

Cho hình chóp S.ABCD có đáy ABCD là hình vuông và \(SA \bot \left( {ABCD} \right)\), gọi O là tâm hình vuông ABCD. Khẳng định nào sau đây sai?

Cho hình chóp S.ABC có \(S A \perp(A B C)\) và đáy ABC vuông ở A . Khẳng định nào sau đây sai ? 

Trong các mệnh đề sau đây, mệnh đề nào là đúng?

Cho hình chóp S.ABC có đường cao SA bằng 2a, tam giác ABC vuông ở C có \(AB=2a,\) \(\widehat{CAB}={{30}^{0}}\). Gọi H là hình chiếu vuông của A trên SC. Tính theo a thể tích của khối chóp H.ABC. Tính cô-sin của góc giữa hai mặt phẳng \(\left( SAB \right),\,\,\left( SBC \right).\)

Cho hai hình vuông ABCD và ABEF cạnh a nằm trên hai mặt phẳng vuông góc. Đường thẳng DE vuông góc?

Cho hai mặt phẳng (P) và (Q) vuông góc với nhau. Người ta lấy trên giao tuyến d của hai mặt phẳng đó hai điểm A và B sao cho AB = 8. Gọi C là một điểm trên (P), D là một điểm trên (Q) sao cho AC, BD cùng vuông góc với giao tuyến d và AC = 6, BD = 24. Độ dài CD là:

Cho tam giác đều ABC có cạnh bằng a và nằm trong mặt phẳng (P). Trên các đường thẳng vuông góc với (P) tại B, C lần lượt lấy D, E nằm trên cùng một phía đối với (P) sao cho \(BD = a\frac{{\sqrt 3 }}{2},CE = a\sqrt 3 \). Góc giữa (P) và (ADE) bằng bao nhiêu?

Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, BC = b, CC' = c. Độ dài đường chéo AC' là

Cho hình lập phương \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}\) . Góc giữa \(A^{\prime} C^{\prime} \text { và } D^{\prime} C^{\prime}\) là

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại \(B,\,\,SA \bot \left( {ABC} \right)\). Gọi E, F lần lượt là trung điểm của các cạnh AB và AC. Góc giữa hai mặt phẳng (SEF) và (SBC) là :

Cho hình chóp S.ABC có \(SA \bot \left( {ABC} \right)\) và đáy ABC vuông ở A. Khẳng định nào sau đây sai?

Cho hình hộp chữ nhật ABCD.A'B'C'D'. Khẳng định nào sau đây không đúng?

Cho hình chóp S.ABC có hai mặt bên (SBC) và (SAC) vuông góc với đáy (ABC). Khẳng định nào sau đây sai?

Cho hình chóp S.ABC có SA = SB = SC = AB = AC = 1, \(B C=\sqrt{2}\). Tính góc giữa hai đường thẳng AB, SC

Cho hình chóp tam giác đều S.ABC với SA = 2AB. Góc giữa (SAB) và (ABC) bằng a. Chọn khẳng định đúng trong các khẳng định sau?

Cho hình lăng trụ đứng \(ABC.ABC\) có đáy là tam giác cân với \(AB=AC=a,\) góc \(\widehat{ABC}={{120}^{0}},\) cạnh bên BB’ = a. Gọi I là trung điểm của CC’. Tính cosin của góc giữa hai mặt phẳng (ABC) và (AB’I)?

Cho tam giác ABC và mặt phẳng (P). Biết góc giữa mặt phẳng (P) và mặt phẳng (ABC) là \(\varphi \). Hình chiếu của tam giác ABC trên mặt phẳng (P) là tam giác A'B'C'.  Tìm hệ thức liên hệ giữa diện tích tam giác ABC và diện tích tam giác A'B'C'.

Cho hình lăng trụ ABCD.A'B'C'D'. Hình chiếu vuông góc của A' lên (ABC) trùng với trực tâm H của tam giác ABC. Khẳng định nào sau đây không đúng?